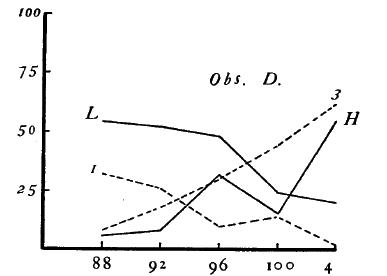
Figure 1.
Relative curves in solid lines, absolute curves in broken lines.
Originally published in Psychological Review, v.35, pages 466-93, 1928.
Ernst Glen Wever and Karl Edward Zener, Princeton University
In certain fields of psychological investigation, chiefly those of feeling and esthetics, there has sprung up, in response to the need for quantification of a special sort, a method of measurement which should rightly be included among the recognized psychophysical methods. The method in its modern form has no generally accepted name; we propose here to call it the method of absolute judgment. The name is suggested by the distinguishing characteristic of the method, that of asking for the rendering of absolute judgments upon single supraliminal stimuli; other methods applicable to supraliminal stimuli require judgments of relation between two (or more) stimuli presented together.
The method of absolute judgment ordinarily is characterized further by its psychophysical function, which is that of determining the rank-order of the members of a group of stimuli; as, e.g. the determination of the relative order of pleasantness of the several members of a group of odors. Whenever, on the other hand, a measure of differential sensitivity is required, one of the relative methods is used. The distinction is not without exception: the method of paired comparisons is a relative method, yet, like the absolute method, its purpose is a determination of the rank-order of stimuli as regards some common feature.
Fundamentally speaking, however, a measure of differential sensitivity is obtainable through any procedure that yields a frequency-distribution of judgments of a certain class as a function of a stimulus-scale. Such a distribution is not necessarily a function of the comparison of stimuli with a fixed standard. It is perfectly possible, as will appear presently, to obtain such a distribution of judgments, and hence a measure of differential sensitivity, through the absolute judgment of single stimuli. Thus it must follow that from considerations of theory the distinction between relative and absolute methods in terms of psychophysical function is not an essential one.
Notwithstanding, the absolute method has been singularly neglected in most discussions of psychophysical procedure. It has had but limited use, and no clear theoretical formulation. Yet the method seems to possess practical possibilities. We propose, accordingly, to enter into a discussion of the method, first, from the viewpoint of its theoretical foundations; and, second, from the viewpoint of the results which it yields as compared with those of another psychophysical method in a field in which each is applicable.
Of what we may call the general method of absolute judgment there have appeared three principal forms. The first of these, the method of choice, was introduced by Fechner in 1871 as a method for experimental investigation in esthetics.[1] According to the method, each of a number of Os was required to choose the most pleasing of a group of simultaneously presented stimuli. The arrangement of the stimuli before each O was haphazard, and was varied for different Os; the relative agreeableness of each stimulus of the group was expressed in terms of the number of first choices which it received.[2]
The serial method appeared in Witmer's study of esthetic forms in 1894 as a modification of the method of choice.[3] The stimuli, instead of being placed before the O in haphazard order, were arranged in a definite, "natural" series; color stimuli, for example, were arranged in order of brightness, or in spectral order, while forms were placed in order of size, or area, or the like. The O then was required to indicate not only his first preference among the stimuli, but his second, third, fourth, and so on, throughout the entire series. This procedure gave an order of preference for each O, and hence diverged from the method of choice, which gave but a composite order for a group of Os.
A year later, in a study of the affective tone of colors, Major used the serial method, but with two important modifications. Arguing that the simultaneous presentation of a series of colors produces undesirable contrast-effects, he resorted to the presentation of the colors one at a time, but in a temporal order corresponding to their position in the spectrum.[4] And, since in a series spread out in time the Os obviously were unable to indicate their order of preference in any direct manner, Major had them judge each stimulus as it appeared in terms of an arbitrary scale running from 1 (very pleasant) through indifference to 7 (very unpleasant). By adding up the scores which each stimulus received in the course of a given number of presentations of the series, and then ranking the stimuli in order of their total scores, the relative affective value of each stimulus was determined. It is plain that the changes instituted by Major considerably altered the task set for the O; indeed, Major himself was dubious whether his procedure could still be regarded as a serial method.
Cohn, in repeating Major's work, further modified the method by the introduction of a certain degree of haphazardness in the presentation of the stimuli.[5] With the use of utterly haphazard presentation, which has come later, the method is so much altered that no longer can it be termed serial; practically it is a new method, and one which may properly be called the method of absolute judgment.[6]
A consideration of the development of the absolute method suggests that the character of the judgment which it requires is at all times fundamentally the same. The judgment expresses a relationship between a particular stimulus and a large series of stimuli presented with or prior to it. In the method of choice the assumption that the series provides the basis of judgment is implicit. With Fechner, as also with Witmer, all the members of the series were simultaneously presented. But with Major they were spread out in time; and here a problem appeared, the problem of the establishment and preservation of the series for the O. The problem was solved in Major's case by a maintenance of the stimuli in orderly sequence, with O's knowledge, obviously to facilitate his conception of them as a series. (Major is careful about the point; see op. cit., 59.) But when Cohn mixed up the stimuli he-- unwittingly, no doubt-- reintroduced the problem of the establishment and functioning of the series for judgment. The problem is still with us: how can the haphazard presentation of single stimuli bring about such a conception of the series as a whole as will serve as an adequate basis of judgment?
Essentially the same question as the one just formulated emerges from a careful analysis of the relative judgment. According to older theory, the comparative judgment arises from the relating of two sense-magnitudes simultaneously present to mind. With simultaneous presentation of the stimuli the process of comparing them seemed to present no difficulty. But when presentation was successive there arose the problem of the persistence of the first impression for the comparison.
With Fechner originated the theory that the first impression is preserved in the form of a memory-image on which the second is superimposed.[7] For almost forty years the Fechnerian theory held sway,[8] until in 1898 Schumann subjected it to attack, maintaining on the basis of introspective evidence that in the majority of cases the presence of a memory-image in the process of comparison cannot be demonstrated.[9] He did not deny some after-effect of the first impression; but he insisted that it need not be conscious.
Schumann's contention was supported in Martin and Muller's experiments with lifted weights, for there it was found that reliable judgments upon a stimulus may be made without obvious reference to a preceding standard stimulus.[10] The basis of judgment in such cases was said to be an absolute impression; i.e. a lifted weight gave rise to an absolute impression, say, of heaviness. That such absolute impressions played an important part in their psychophysical situation was indicated by characteristic tendencies in the judgments, tendencies which could not be explained in terms of the familiar Fechnerian errors. (The tendencies were of two kinds, a general tendency which was the same for all Os, and typic tendencies which varied for different Os. See op. cit., 21ff.) The findings in lifted weights were verified by later investigators, and the influence of the absolute impression was demonstrated in a number of other fields.[11]
The psychological basis of the absolute impression remains to be defined. In the discussion of Martin and Muller the suggestion appears that it is a function of the physical characteristics of the O and of his past experience in dealing with objects. That experience with stimuli in daily life is a factor in determining the absolute impression seems a reasonable claim, but it is likely also that during an experiment the members of the series presented would have considerable influence. It seems probable that the absolute impression is no constant affair, but is responsive to a change in the magnitude or the range of the stimuli used in a given situation. Indeed, we are confronted here with the same problem that arose in our consideration of the absolute judgment, the problem of the manner of establishment, through the presentation of members of a stimulus-series, of a basis for the absolute factor in judgment.
If, as we have stated, an absolute judgment expresses a relationship between a present stimulus and a whole series of stimuli, then it is plain that the ability of the O to make the judgment presupposes some sort of knowledge of that series. His previous experience with a body of stimuli of ranging magnitudes makes possible the assignment to an incoming stimulus of a more or less definite position in the total range of magnitudes. Just what is the nature of the mental formation through which knowledge of the series is carried is a problem of considerable interest. Introspection discloses that at times the series is represented by a mental image, and that in rendering a judgment the O relates the incoming stimulus to this image. Frequently, however, the presence for the O of any imaginal representation of the series fails to be revealed, though absolute judgments are made with complete readiness. Indeed, as an experiment progresses and an O becomes automatized in his task, the general tendency seems to be for any imaginal representation to disappear. There is in such case, however, no impairment of O's capacity to judge; there is no noticeable change either in the distribution of the judgments or in the ease of making them. Clearly, introspection is no safe index of the presence of a mental formation adequate to the absolute judgment: the judgment appears in the complete absence of any content obvious to introspection. One must infer the presence of such a mental formation simply on the basis of the O's capacity to judge.
The mental formation that serves as a basis for the rendering of absolute judgments we propose to call an absolute series. The expression reflects the essential characteristic of the formation: it suggests a correspondence between the actual range of stimuli and O's conception of the stimuli as a series. Such a correspondence is a fact that is readily demonstrated in an experimental situation. After the presentation of a series of stimuli, say, of squares ranging from 10 to 20 cm. on a side, the O retains a conception of the stimuli as a series; and this is true whether in the presentation they have appeared in order of magnitude or have been quite haphazard. O will be able to demonstrate his knowledge of the general order of magnitude of the stimuli, of the approximate range of magnitudes, and perhaps also something of the internal structure of the series. In the above case, for example, he will be able roughly to indicate, by drawing or description, the general size of the squares, their variation in size, and possibly that, let us say, the smaller squares appeared with the greater frequency.
The absolute series should be considered in relation to the formation, not only of absolute judgments, but of relative judgments also. As shown above, work with the relative method yields evidence suggesting that in certain instances an absolute series becomes established and plays an important role in determining judgment. A case in point is Martin and Muller's absolute impression, which can readily be accounted for in terms of our theory as a relation between the given stimulus and a previously established absolute series.
In the use of the absolute method in psychophysics one finds that the O can make adequate judgments upon the members of a stimulus-series only after he has become familiar with the general range of that series. In certain settings, as, e.g. in experiments on affection where judgments of pleasantness or unpleasantness are required, familiarity with the stimulus range has already been built up in past experience, and in judging the O is, in effect, relating the present stimuli to that range. (Strictly, this statement holds only at the beginning of an investigation, for as experimentation proceeds the judgments become more and more a function of the particular stimuli presented.) Usually, however, the series of stimuli concerned in the experiment at hand must be presented entire or in large part before the O's judgment can be considered reliable.
The writers have in practice found it to be good technique to require the O to begin judging with the very first stimulus presented, notwithstanding the fact that at this time he may have no notion of the stimulus-range. If in the attempt to establish an absolute series the stimuli are presented without any requirement of judging, considerable time is wasted. The attitude of experiencing without judging is different from that of experiencing to judge. The second attitude favors the early growth of O's confidence in his adequacy to the task; while the first attitude, on the other hand, leads him (particularly if he be unpracticed) to demand an unduly secure grasp of the series before committing himself in judgment. It is clear in theory that for preliminary presentation to be of greatest effectiveness it must occur under precisely the same circumstances and under the same attitude of the O as are intended for the experiment proper, and that any clue to the O of a transition from preliminary to main experiment should be strictly avoided. Actually, the point of transition can best be determined by the E, after the experiment is concluded, on the basis of a statistical examination of the data.
The requirement of judging before an absolute series has become established presents no practical difficulty. The first judgment, it is true, must be merely random. Ordinarily the O responds with the middle of possible categories. After a strikingly small number of presentations, however, his judgments become stabilized, showing the ready development of the absolute series. The rapid growth of the absolute series is favored by the early presentation of the extreme members of the body of stimuli. At no time, strictly speaking, can it be regarded as established finally; the fact is obvious that it is a continuous function of stimulus-presentation. Practically, however, with the same set of stimuli the change after the first preliminary period is inappreciable.
The rate of establishment of the absolute series no doubt varies with the kind of stimuli used and with the arrangement of the stimulus-series. In the field of tonal pitch the rate of development of a basis for absolute judgment has been investigated by Truman and Wever,[12] who presented singly five different tones by the method of constant stimuli, and showed that reliable absolute judgments occurred after but very few presentations. Indeed, the absolute series was so readily established that, without any preliminary practice, results from the first 25 presentations were indistinguishable from those of the second 25. The present writers have observed a similar phenomenon in the field of lifted weights (Infra, p.477); here also reliable absolute judgments occur after but a few presentations. A full and systematic investigation of the factors influencing the rate of establishment of an absolute series has yet to be made.
The extent to which an absolute series may hold over from one experimental session to the next is a second problem, and, here particularly, empirical evidence is meager. Moreover, a precise determination of the amount of persistence of the absolute series in any given case will be difficult in proportion to the rapidity of its initial establishment. The measure of persistence must be expressed in terms of a difference between the rates of establishment of the absolute series in successive sittings, and the greater the initial rate the less the possible difference and hence the greater the likelihood of an obscuring of a difference by experimental error. In the use of the absolute method with weights and with tonal sequences judged as to finality the writers have observed that reliable judgments appear earlier in successive sessions of an investigation, suggesting that the absolute series persists in some degree from one session to the next. These observations are but casual, however; the problem calls for direct experimental attack in a variety of fields.
Indirect evidence of the persistence of an absolute basis of judgment may be obtained from a consideration of the results of the relative method when the time-interval between standard and comparison stimuli is large. It has been shown in a number of experiments[13] that delay as long as one to five minutes in the presentation of the second stimulus does not greatly reduce the accuracy of judgment. The same is true even when the interval is filled with distraction. The indications are that judgments under these conditions are not relative in the usual sense, but are absolute. Indeed, it was reported in the study by Fullerton and Cattell (op.cit., p.149) that the standard did not persist through the interval in the form of a memory-image, but rather that each stimulus was "decided" separately and that these "decisions" were compared for judgment. Angell (op.cit., p. 69f.) had a similar explanation; the judgments were designated as "free" in the sense of lacking any imaginal basis (cf. Martin and Muller's "absolute impression"). In the writers' view these facts are to be explained in terms of the establishment, and preservation through the interval, of an absolute series which serves as a basis for judgment.
Though it seems probable that the absolute series may remain relatively stable over a considerable interval, it may show nevertheless a ready response to the presentation of a new range of stimuli. This fact is illustrated by the following experiment.
Using an absolute procedure (outlined in Experiment II. below), an O was given a "light" series of weights (84, 88, 92, 96, and 100 grams) and after his judgments had become stabilized, a "heavy" series (92, 96, 100, 104, and 108 grams) suddenly was introduced. The effect of the first series on the judgments of the second was quite evident for 20 or 25 presentations, i.e. for four or five rounds judgments of "heavy" predominated for all the stimuli; from this point on, however, the judgments showed a redistribution conforming to the second stimulus-series.
Results similar to the above were shown in the experiment of Truman and Wever, (op.cit.) in which a "normal" series of five pitches was followed by a "displaced" series, and the judgments after two or three rounds showed a redistribution corresponding to the new set of stimuli.
The effects of shifting the stimulus-series have been disclosed in other fields. In the estimation of magnitudes, Hollingworth has found that the constant errors of estimation are a function of the series of stimuli.[14] The greater magnitudes tend to be underestimated and the smaller magnitudes overestimated, with an indifference-point in the middle of the series. If the stimulus-series is shifted or extended the distribution of errors shifts accordingly, which means that the indifference-point maintains a constant relation to the series as a whole. The phenomenon is clearly a function of the presence of a series of stimuli, for considerable constant errors do not occur in the estimation of a magnitude taken out of relation to a series. These findings Hollingworth explains as due to a "central tendency of judgment," a tendency for the judgment upon each magnitude in the series to be deflected toward the midpoint of that series.[15] According to Hollingworth, the deflection of judgments is produced through the operation of a mental set corresponding to the stimulus-series. This "mental set" is essentially what we have called an absolute series, and in Hollingworth's data its ready responsiveness to an extension or shift of the stimuli is clearly evident.
In the above discussion the absolute series has been postulated as a basis for the formation of absolute judgments, and certain of its fundamental properties have been considered. The significance of the absolute series in experimental situations will be revealed in the application of the method of absolute judgment to the solution of psychophysical problems.
The method of absolute judgment has developed in response to the need for quantification in fields in which other measurement-methods are ineffective (see, however, note 1). The use of the method has always been rather restricted, which may in part explain the fact that there has been no thoroughgoing comparison of its results with those yielded by other psychophysical methods.[16] It is quite apparent that such a comparison would lead to a clearer evaluation of the method and of its systematic position in the psychophysical field. Consequently, in experiments with lifted weights the writers have sought to compare results obtained by the method of absolute judgment with results obtained by the method of constant stimuli. Two experiments were performed, differing slightly in their settings. (The first experiment was performed in the Harvard Psychological Laboratory in 1926, the second in the Princeton Psychological Laboratory in 1927.)
As stimuli were used a number of weights: 88, 92, 96, 100, 104 grams; the weights were of hard rubber, 2.5 in. in diameter and 1 in. high, and were arranged on a weight-table in the usual manner. The order of presentation was regulated so as to neutralize the effect of contrast.[17]
The Os were Fl. R. De Silva (D), H. E. Israel (I), R. A. McFarland (M), F. A. Pattie (P), and the writers (W and Z).
There were two procedures. In the procedure with the method of constant stimuli the 100-gram weight was given as standard, and was always lifted first. the O was instructed to judge, with the criterion of objective weight[18], in terms of "heavier," "equal," and "lighter"; in case of a judgment of "doubtful" the presentation was repeated. In the procedure with the method of absolute judgment the five weights were used without any standard. the O was required to make absolute judgments, using in his report the categories "one," "two," and "three" to include the series from light to heavy in the order named, with the step from "one" to "two" equal to that from "two" to "three."
Every O was used with both of the above procedures; for I, P, and Z the experimental session with absolute judgments preceded that with relative; for the remaining Os the order was reversed. Except for W and Z the Os were without knowledge of the object of the investigation. In both procedures the O was given a short period of preliminary practice, and then 50 judgments were taken on each stimulus (or comparison-pair).
For every O the distributions of judgments with both relative and absolute methods are shown in the form of curves, Figs. 1-6. Stimulus-values are shown in grams along the abscissa, and frequencies of judgment in percent along the ordinate. The curves for the relative method are drawn in solid lines, those for the absolute method in broken lines. The symbols indicate the judgment which the particular curve represents: "lighter" (L), "heavier" (H), "one" (1), "three" (3).

Figure 1.
Relative curves in solid lines, absolute curves in broken lines.
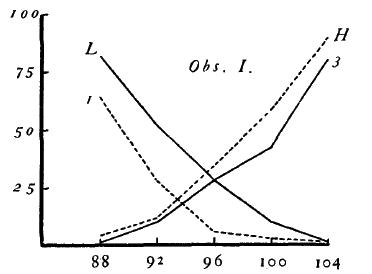
Figure 2.
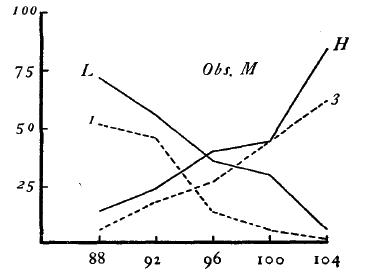
Figure 3.
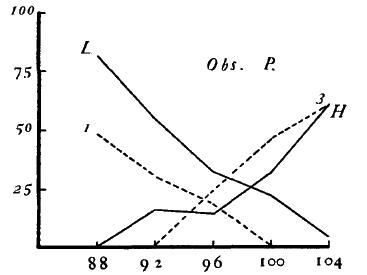
Figure 4.
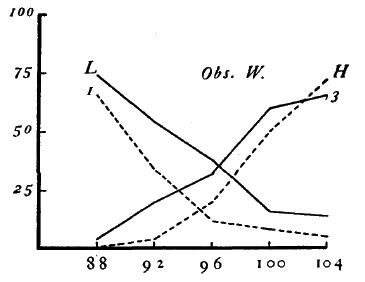
Figure 5.
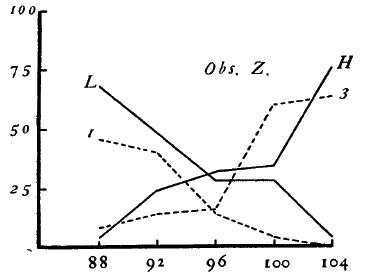
Figure 6.
The data obtained by the relative method were treated statistically by the customary constant-stimulus process (after Urban), the values of h, the measure of precision, and of C, the 50 percent crossing-point of the ogive fitted to the distribution, being determined for judgments of "lighter" and of "heavier" for every O. Moreover, for purposes of comparison, like values were computed from the distributions of judgments of "one" and "three" as obtained by the absolute method. The results of the above calculations are shown in Table I. In the first column is given the name of the O. Column 2 indicates whether the method of procedure was relative (Rel.) or absolute (Abs.). Column 3 gives the categories of judgment: "lighter" (L), "heavier" (H), "one" (1), "three" (3). C and h occur in the 4th and 5th columns, respectively. The remaining columns show the degree to which the curves approach normality (column 6), the values of the intervals of uncertainty (column 7), and the measures of the points of subjective equality (column 8); the significance of these will be made clear in the discussion below.
Table I.
| C | h | Sigma(p'-p)^2 | IU | PSE | |||
| D | Relative | L | 91.6 | .05 | .022 | 9.3 | 99.3 |
| H | 104.9 | .07 | .047 | ||||
| Absolute | 1 | 82.3 | .05 | .007 | 18.9 | 93.2 | |
| 3 | 101.2 | .07 | .000 | ||||
| I | Relative | L | 92.5 | .12 | .002 | 7.4 | 96.1 |
| H | 99.9 | .12 | .011 | ||||
| Absolute | 1 | 89.5 | .15 | .001 | 8.7 | 93.5 | |
| 3 | 98.2 | .13 | .004 | ||||
| M | Relative | L | 93.4 | .08 | .009 | 4.7 | 95.8 |
| H | 98.1 | .08 | .039 | ||||
| Absolute | 1 | 89.4 | .10 | .015 | 12.1 | 94.8 | |
| 3 | 101.5 | .08 | .004 | ||||
| P | Relative | L | 93.4 | .13 | .016 | 9.6 | 97.1 |
| H | 103.0 | .08 | .017 | ||||
| Absolute | 1 | 87.4 | .08 | .009 | 14.1 | 94.8 | |
| 3 | 101.5 | .08 | .021 | ||||
| W | Relative | L | 93.1 | .08 | .005 | 5.4 | 95.8 |
| H | 98.5 | .08 | .008 | ||||
| Absolute | 1 | 90.0 | .11 | .005 | 10.6 | 95.5 | |
| 3 | 100.5 | .13 | .002 | ||||
| Z | Relative | L | 92.0 | .08 | .014 | 8.2 | 96.2 |
| H | 100.2 | .08 | .017 | ||||
| Absolute | 1 | 87.0 | .07 | .015 | 13.4 | 94.5 | |
| 3 | 100.5 | .09 | .033 |
As stimuli in this experiment seven weights were used: 84, 88, 92, 96, 100, 104, and 108 grams. The Os were C. W. Bray (B) and H. Schlosberg (S).
The instructions for the relative procedure were as in Experiment I. For the absolute procedure they differed from the previous ones only in that the categories of judgment were "heavy," "medium," and "light"; and in that no instruction was given as to the steps between the categories.
Each O served under both procedures; the procedures were alternated in separate experimental sessions until 100 rounds of one judgment per stimulus (or comparison-pair) were obtained under each.
In all respects besides those indicated the conditions in Experiment II were the same as in Experiment I.
The psychometric curves are shown in Figs. 7-8. The construction of these figures follows that of the previous ones, except that for curves of the absolute judgments, symbols I and h are used to represent "light" and "heavy," respectively. For the calculated results, see Table II., the arrangement of which is the same as that of Table I., except for the change of symbols just mentioned.
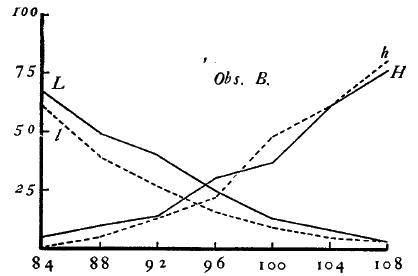
Figure 7.
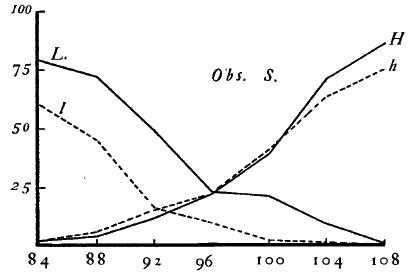
Figure 8.
Table II.
| C | h | Sigma(p'-p)^2 | IU | PSE | |||
| B | Relative | L | 88.5 | .07 | .002 | 13.1 | 95.3 |
| H | 101.6 | .07 | .040 | ||||
| Absolute | 1 | 85.8 | .06 | .003 | 15.4 | 94.8 | |
| 3 | 101.2 | .09 | .004 | ||||
| S | Relative | L | 91.7 | .08 | .012 | 9.1 | 96.7 |
| H | 100.8 | .10 | .007 | ||||
| Absolute | 1 | 86.1 | .10 | .003 | 15.7 | 93.2 | |
| 3 | 101.8 | .08 | .003 |
A consideration of the data as shown in Figs. 1-8 brings out some striking relationships between relative and absolute methods. These relationships will be discussed under two heads. The first, (A), will involve the degree to which the curves approach normality and the degree of precision manifested. The second, (B), will include the values of C, the 50 percent crossing-points of the curves, and along with them the intervals of uncertainty and the points of subjective equality. The discussion under the latter head will reveal some interesting differences between relative and absolute methods, differences which will give insight into the fundamental nature, not only of the absolute method, but of the method of constant stimuli as well.
A. The curves obtained with the absolute method, like those with the relative, appear in most cases to approximate the ogival form. For certain of the Os, B, S, I, and W, the curves are quite regular, for M and Z they are less so, while for P and D they are rather ragged. The smoothness or irregularity of the curves seems predominately a function of the O rather than of the method. In general, if for one method an Os curves tend to approximate normality, those for the other method do also. It should be noted, however, that the factor of practice enters and to some extent obscures this tendency. (In D's case in particular this factor may in part account for the unusual increase in smoothness of the absolute curves over the relative.)
The degree to which the two sets of curves tend to approximate normality may perhaps better be expressed in statistical terms. In Tables I. and II., column 6 shows, for each distribution, the values of the sums of the squared deviations of the obtained percentages from the theoretical (Sigma(p'-p)^2). (It should be borne in mind that for a perfect fit Sigma(p'-p)^2 becomes zero.) An examination of these columns confirms our inference from inspection of the curves, for most of the measures indicate a fairly high approximation to normality, and the values for the absolute method are as good, if not better, than those for the relative. The fact that most of the curves with both relative and absolute methods are practically normal justifies us in the use of Urban's process for these curves, and hence, under the assumptions of our discussion, permits a comparison of the two methods in terms of the measures which that process yields. We give the values obtained from the "ragged" curves also, for what they are worth; they obviously are not to be taken too seriously. The reader can always go back to the raw data as shown in Figs. 1-8.
A consideration of the values of h, the measures of precision, as given in the 5th columns, Tables I. and II., shows that practically the same degree of precision is afforded by the two methods. It is evident that there is no general tendency for corresponding values of h to be greater for either of the two methods. This fact becomes rather significant if one allows the contention sometimes made that Ii (or one of its simple functions) rather than the 'difference limen' (DL), is a measure of the sensitivity of the subject[19], for it means that for such a determination one method is little different from the other.
B. A comparison of the two methods as regards values of C (column 4, Tables I. and II.) reveals an interesting fact. The "H" and "3" values (in Table II., "H" and "h") agree fairly closely, but in every instance the "1" (or "l") values are less than the "L" values. This situation shows in the figures (Figs. 1-8), as the "1" (or "l") curves are usually shifted to the left as compared with the "L" curves. This difference in the curves for absolute and relative methods may be accounted for if one supposes that there is, in the absolute method, (1), a spreading apart of the curves, due to a greater abundance of intermediate judgments, and (2), a shift of the curves downward in the intensity-scale, resulting from a general increase in the effective intensity of stimuli. It is apparent that for the curves of the "heavy" judgments these two influences are opposed: the first would tend to shift the curves to the right (as the scales are shown in the figures), while the second would tend to shift them to the left, and if the two factors were of about equal effectiveness the obtained curves would show no significant change. The curves of "light," on the other hand, would be moved to the left by both these influences, and should show a considerable change. Actually, as mentioned above, the "heavy" curves show no significant change, while the "light" curves are shifted downward quite noticeably.
(1) An examination of the data shows at once that the first of the above suppositions is true; in the absolute procedure there is a much greater abundance of intermediate judgments, as is clearly shown by the greater values of the intervals of uncertainty (IU), given in the 7th columns of Tables I. and II.
(2) A consideration of the second supposition leads one to the measures of the points of subjective equality (PSE), column 8 of Tables I. and II., for it is in these that a general shift would be expected to show. Our theory is sustained in every case: for each O the PSE is lower for the absolute method. Comparison of results of the two methods is made easier in Fig. 9, where the PSEs for the relative method are plotted along the upper scale, and those for the absolute method along the lower. For every O there is a shift to the left from relative to absolute.
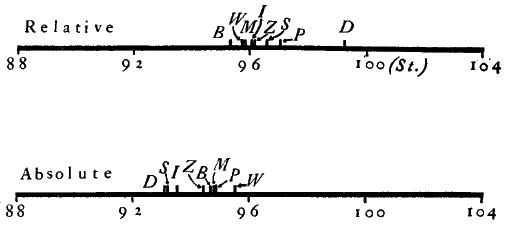
Figure 9.
It is significant to note further that for the relative method the PSEs cluster about 96, which is the midpoint of the stimulus-series, while for the absolute method the PSEs are grouped in the region of 94. That in the absolute procedure the points of subjective equality are all below the midpoint of the stimulus-series is a very interesting fact. This situation is what we would have expected to find in the relative procedure if we had used the same series, but with the standard at 96 (the midpoint) instead of at 100. We had used the plan of shifting the standard upward, as has been customary since Urban[20], because we thought that such a shift compensated for the time-error introduced by lifting the standard always before the comparison weight.[21] That this shifting of the standard was generally effective is quite apparent, for the PSEs (all except D's) cluster closely about 96, reflecting the fairly symmetrical distribution of the judgments in the series. With the standard at 96, on the contrary, the PSEs would have been shifted downward, due to a predominance of judgments of "heavier."
It is surprising to find, in the results of the absolute method, where no standard is present, a skewness of just the kind that the above shifting of the standard in the relative procedure was devised to correct. It would seem that the phenomenon goes beyond the mere matter of the temporal order of standard and comparison.
It is suggestive to note also that the appearance of this so-called time-error in the relative procedure is by no means confined to the field of lifted weights. Köhler found it, for example, in the judgment of tonal intensity[22]. The phenomenon he sought to explain by postulating, first, that the one stimulus, the standard, leaves behind it a certain "sediment" which functions for the comparison; and, second, that this sediment "settles" as time goes on, thus reducing its effective intensity, and in consequence relatively enhancing the intensity of the second tone (Idem, 166ff).
Moreover, Köhler suggested that the absolute impression which occurs in the relative procedure may be said to be due to the formation of a "general level" of sediment (Idem, 172f.). To explain our present findings with the absolute method we need go but a step farther along the same line of theorizing; let us suppose that there occurs as the experiment progresses a gradual sinking of the general level that serves as the basis of absolute judgment. Or, in terms of our own theory, there is a constant tendency for the absolute series as a whole to move downward in the intensity-scale. Obviously, the result of any such constant tendency would be to bring each succeeding stimulus into relation with an absolute series which is shifted downward with respect to the scale of physical intensities. And as the stimulus is judged with respect to an absolute series that is "too low," the results, in consequence, would show a predominance of judgments of "heavy," as is actually the case.
It is plain that the differences exhibited between the points of subjective equality in the two procedures are not significant in relation to the fundamental character of the methods, but are rather a consequence of an arbitrary displacement of the standard in the relative series. The one remaining difference of importance in the two methods is, then, if our above analysis is correct, the difference in the proportion of intermediate judgments. Is this difference an essential one?
We believe that the proportion of intermediate judgments made under the absolute procedure is determined chiefly by the attitude of the O; in the first experiment we sought by instruction to regulate the factor of attitude so that the intermediate category would be on a par with the other categories. Such an attitude seemed the most natural for the method. There is every indication that this attitude was maintained in Experiment I., and in Experiment II. also, though there it was not asked for in the instructions. In consequence, the number of intermediate reports was large. We are confident that by proper instruction Os attitude could have been changed so as to alter the number of intermediate judgments in either direction.
Certainly one can do so in the relative procedure. The fact is notorious that in the method of constant stimuli the proportion of equal judgments is a function of the attitude of the O. A "liberal" attitude occasions a large number of reports of "equal," while a "conservative" or "critical" attitude gives a smaller number.[23] Indeed, in some instances such reports occur but rarely, or not at all.[24] Because of these facts we do not believe the difference here obtained in the frequencies of intermediate judgments for relative and absolute methods to be a fundamental difference between the methods; nor do we consider the problem of the control of observational attitude a more serious one in the absolute method than it is in the relative.
In any case, if one measures sensitivity in the customary manner, in terms of the "difference limen," the problem of attitude is a very serious one indeed. Plainly, since the magnitude of the DL is intrinsically dependent upon the proportion of intermediate judgments, it follows that with this criterion sensitivity is a direct function of observational attitude. This deduction, we know, runs against an assumption implicit in psychophysical determinations in general, the assumption that sensitivity is something of definite nature, basic to the organism, and expressible in fairly precise terms, and not simply a kind of shadow-shape that any wind of instruction or set can fashion to its caprice.
The situation is this, that if we are to admit sensitivity as a real entity, measurable within allowable limits of variation, we must either so carefully control attitude that its variations cause no considerable change in the DL[25], or else supplant the DL with a new measure of sensitivity which is not so much subject to alteration by attitudinal change.
The first solution is counseled by George, who thought that much of the equivocality of the equal judgment could be eliminated by a careful restriction of what is to be reported as "equal." We are quite free to admit that restriction of the equal category is a great improvement, but we believe nevertheless that the desired end of constancy of measurement has by no means been obtained thereby.
We believe that in practice the above two solutions will reduce to one, for we know of but a single truly effective way to control attitude in regard to intermediate judgments, and that is so to dispose the attitude as to eliminate such judgments entirely. It is perfectly feasible; in the instruction one needs simply to state that a judgment of "equal" is not allowed, and that report is to be made in terms only of "greater" and "less." For obvious reasons it is advisable further to state that no two stimuli will be really equal, and that when in doubt the O is to guess. The remarkable fact is that the forced judgments under such circumstances are more often right than wrong[26]. O is seemingly demonstrating greater sensitivity than with the usual procedure. But his sensitivity as measured by the DL has become infinite: the DL has reduced to zero along with the intermediate judgments!
Of course, we could not take seriously a measure of sensitivity at infinity, but would prefer rather to call it indeterminate, and seek for a new measure. As such a measure, h, the measure of precision of the psychometric function, has already been suggested. It is a measure of the steepness of the psychometric curve, i.e. it expresses the rate of change of the frequency of judgments of a certain category as a function of change of stimulus, and this, we think, is just what a measure of sensitivity ought to do. The measure seems sound in theory, but at the present time we have no further justification of its use[27]; we hope that there soon will be forthcoming experimental data sufficient to form a real test of the validity of this measure as against the traditional measure, the limen.
We seem in this discussion of fundamentals to have wandered far from the question of the properties of the absolute method. Actually, however, the method has remained in the field of our attention, for the discussion involves it as much as it does the method of constant stimuli. If one is to admit an intermediate category, and seek to control the attitude with which it is regarded, then, we think, the best procedure is to define the attitude as we have in Experiment I., for such an attitude seems a simple and natural one, easy to maintain. But we are particularly interested here in the second type of solution mentioned above, the possibility of eliminating intermediate judgments entirely, allowing merely judgments of "greater" and "less," and using as a measure of sensitivity the precision-values of the psychometric functions obtained. How constant such determinations will be, and how well they will agree with determinations by the constant-stimulus procedure with two categories remains to be discovered.
The data which we have, so far as they go, warrant us in concluding that the fundamental natures of the method of constant stimuli and the method of absolute judgment are much the same. Consequently, we are led to hold that the absolute method is a perfectly practicable method for the determination of sensitivity, a method worthy of being set alongside the method of constant stimuli for this purpose.
In this paper the method of absolute judgment has been considered, first, from the standpoint of theory; and, second, from the point of view of its use as a practical instrument for the solution of psychophysical problems.
1. The method of absolute judgment consists in the single presentation of members of a stimulus-series, and the requirement in each case of a judgment in absolute terms. Such judgment is possible through the establishment for the O, by the presentation of a series of stimuli, of a certain degree of knowledge of that series. The body of knowledge of the series that is adequate to absolute judgment we have called an absolute series.
2. Certain basic properties of the absolute series have been discussed: the manner of its establishment, its persistence, and its responsiveness to a change in the stimulus series.
3. The psychophysical characteristics of the method of absolute judgment have been set forth by comparing the method with the method of constant stimuli in a typical experimental situation. Psychometric curves were obtained by both methods, and it was demonstrated that the curves are significantly alike.
4. Certain differences in the results point to a difference, not in the fundamentals of the methods, but a difference of attitude affecting the frequency of intermediate judgments. This matter of attitude raises a problem of crucial importance to psychophysics in general, the problem of a proper measure of differential sensitivity. Suggestions are made for the adequate solution of this problem.
5. The method of absolute judgment is regarded, on the basis of the evidence, as a practicable method for use in psychophysical investigation.
1. Fechner, G. T., "Zur experimentalen Aesthetik," Abh. d. k. sãchs. Gesellsch. d. Wiss., math.-phys. Cl., 1871, 9, 602f. [Return to text]
2. For illustration of the technique see Fechner, "Vorschule der Aesthetik," 1879, I, 193f. [Return to text]
3. Witmer, L., "Zur experimentellen Aesthetik einfacher räumlicher Formverhältnisse," Phil. Stud., 1894, 9, 122ff., 209ff. In his treatment of affective methods Külpe a little earlier had discussed what he called a "serial method," and had wrongly identified it with Fechner's method of choice ("Grundriss der Psychologie," 1893, 239f., 244). Külpe's method really involved a new feature, the requirement of the O to arrange the stimuli in order of preference. (In later discussions this has been called the method of arrangement.) [Return to text]
4. Or in order of saturation, etc. Major, D. R., "On the affective tone of simple sense-impressions," Amer. J. Psychol., 1895-6, 7, 57ff. [Return to text]
5. He retained a serial order of presentation of the brightnesses of a given hue, but the presentation as regards hue was haphazard. Cohn, J., "Gefühlston und Sattigung der Farben," Phil. Stud., 1900, 15, 279-286. [Return to text]
6. The use of completely haphazard presentation was first suggested by Cohn, see op. cit., p. 286. For a recent use of the method in its modern form, see Young, P. T. "Constancy of affective judgments to odors," J. EXPER. PSYCHOL., 1923, 6, 182f. [Return to text]
7. "Elemente der Psychophysik," 1860, I, 88. [Return to text]
8. Cf., e.g. Stumpf, C., 'Tonpsychologie,' 1883, I, pp. 98f.; Lehmann, A., "Kritische und experimentelle Studien über das Wiedererkennen," Phil. Stud., 1892, 7, 205. [Return to text]
9. Schumann, F., "Zur Psychologie der Zeitanschauung," Zsch. f. Psychol., 1898, 57, ,,8ff.; Beiträge zur Analyse der Gesichtswahrnehmungen III, Der Successiv-vergleich, ibid., 1902, 30, 241-291. See also, Külpe, O., "Aussichten der experimentellen Psychologie," Phil. Monatshefte, 1894, 30, 282f.; Angel;, F., "Discrimination of clangs for different intervals of time," Amer. J. Psychol., 1900, 52, 69ff. [Return to text]
10. Martin, L. J., and Muller, G. E., "Zur Analyse der Unterschiedsempfindlichkeit", 1899, 43ff. [Return to text]
11. In the following, at least: lights, esthesiometry, time-intervals, clangs, sound-intensities, and visual distances. Titchener gives the references: "Experimental Psychology," 1905, II, ii, p. 304, note 5. [Return to text]
12. Truman, S. R., and Wever, E. G., "The judgment of pitch as a function of the series," Univ. Calif. Publ. Psychol., 1928, 3, 215-223. [Return to text]
13. Fullerton, G. S., and Cattell, J. McK., "On the perception of small differences," 1892, pp. 147ff.; Baldwin, J. M., and Shaw, W. J., "Memory for square size," Psychol. Rev., 1895, 2, 236-9; Angell, F., and Harwood, H., "Experiments on discrimination of clangs for different intervals of time," Amer. J. Psychol., 1899, 11, 67-79; Angell, F., op. Cit. in note 11, 58-79. [Return to text]
14. Hollingworth, H. L., "The inaccuracy of movement," Arch. Psychol., 1909, 2, No. 13, 21-39; "The central tendency of judgment," J. Phil., 1910, 7, 461-9. [Return to text]
15. A similar phenomenon had been noted earlier by Warren and Shaw in the comparison of squares, 'Further experiments on memory for square size,' Psychol. Rev., 1895, 2, 239-244. [Return to text]
16. There has been some comparison of the method of paired comparisons with forms of the absolute method. See Witmer, L., Phil. Stud., 1894, 9, 122ff., and Cohn, J., Phil. Stud., 2900, 25, 282ff. [Return to text]
17. For a description of the weights, see Fernberger, S. W., "A new form of stimuli for lifted weight experiments," Amer. J. Psychol., 1920, 31, 147-151. For the regulation of contrast-effects, see Fernberger, "Interdependence of judgments within the series for the method of constant stimuli," J. EXPER. PSYCHOL., 1920, 3, pp. 127, 148-9. [Return to text]
18. Fernberger, S. W., 'An experimental study of the "stimulus error," J. EXPER. PSYCHOL., 1921, 4, 63-76. [Return to text]
19. The use of h as the measure of sensitivity is as old as Fechner. See "Revision der Hauptpuncte der Psychophysik," 1882, p. 48f. More recently, G. H. Thomson, in "A new point of view in the interpretation of threshold measurements in psychophysics," Psychol. Rev., 1920, 27, 300-307, has argued for the use of the interquartile range, and E. Culler, in "Studies in psychometric theory," Psychol. Monog., 1926, 35, No. 163, 115-122, has extolled the merits of the probable error. (Both the inter-quartile range and the probable error bear a simple mathematical relation to h.) [Return to text]
20. Urban, F. M., "The application of statistical methods to the problems of psychophysics," 1908, p. 11. [Return to text]
21. See, in regard to the time-error, Fechner, "Elemente der Psychophysik," 1860, I, 112ff., and Martin and Muller, "Zur Analyse der Unterschiedsempfindlichkeit," 1899, 58ff. [Return to text]
22. Köhler, W., "Zur Theorie des Sukzessivvergleichs und der Zeitfehier," Psychol. Forsch., 1923, 4, 115-175; see also the references cited on p. 115. [Return to text]
23. See Washburn, M. F., "An instance of the effect of verbal suggestion on tactual space perception," Amer. J. Psychol., 1909, 20, 447f.; Brown, W., "The judgment of difference," Univ. Calif. Publ. Psychol., 1910, 1, 30-33; Fernberger, S. W., "The effect of the attitude of the subject upon the measure of sensitivity," Amer. J. Psychol., 1914, 25, 538-543; Woodworth, R. S., "Professor Cattell's psychophysical contributions," Arch. Psychol., 1914, 4, No. 30, 66f.; and Thomson, G. H., op. cit., 301f. [Return to text]
24. Brown, W., loc. cit.; Fernberger, S. W., "On the elimination of the two extreme intensities of the comparison stimuli in the method of constant stimuli," Psychol. Rev., 1914, 21, 353f. [Return to text]
25. See George, S. S., "Attitude in relation to the psychophysical judgment," Amer. J. Psychol., 1917, 28, 1-37. [Return to text]
26. This is admirably shown in Brown's experiment, be. cit.; see especially p. 33. Cf. also, Fullerton and Cattell, "On the perception of small differences," especially p. 127. [Return to text]
27. Culler, E. (op. cit.) has elaborated four reasons for the use of the probable error (which ought, of course, to apply equally to h); these reasons, however, do not impress us as of major importance. [Return to text]