Acoustic Learning,
Inc.
Absolute Pitch research, ear training and more
I've been thinking about word acquisition and concept-- specifically, that one doesn't exist without the other.
Words exist to mediate concepts. Even words which may not have a literal definition, like "the", possess some functional usage which is a valid concept. Language and culture act cyclically to introduce, validate, and reinforce important concepts; that is to say, concepts may exist without words, but words come into being to describe concepts as needed, and thus words cannot exist independently of the concepts they describe. One of the chapters in the book explains how words aren't learned from dictionary definitions-- or, if they are learned, they are learned imprecisely (resulting in semi-correct usage like "the tree appended a branch"). I've always been skeptical of word-a-day calendars or other "vocabulary-building" devices because I've instinctively felt that vocabulary is developed from exposure to verbiage in meaningful context; the book confirms my suspicion by illustrating how a dictionary definition typically fails to impress the precise concept underlying a word.
And what about non-word components, like "ba" or the plain letter R? These do still possess conceptual value. R is, if nothing else, "the letter between Q and S", and "ba" could be either a sound effect, a baby noise, or an exclamation of disapproval. The fact is that if I hear any language sound, I could describe to you what concept it may represent. Although phonemes have been described as physically distinguishable by "mere otherness", think of the extraordinary effort applied in early years toward forming letter concepts, giving each letter its own personality and identity. L and X aren't just funny sounds whose differences have to be memorized by rote and picked out by constant drilling and testing; they're "Rebel L" and "X marks the spot." You don't mark a spot with an L; you don't sing about a "Rebel X". The concepts don't fit.
So I suddenly find myself asking, with musical ear training: where are the concepts? When I recognize two words-- say, "ball" and "tall"-- one of the sounds evokes the idea of a sphere, and the other indicates an attribute of physical height. I'm not trying to "tell them apart", because each sound represents a completely different concept. I'm not comparing the two sound masses to figure out which one has a b and which one has a t; indeed, the thought of doing so seems patently ridiculous. This is, however, exactly the kind of process expected in musical ear training-- at least, I've encountered plenty of ear training methods and programs which attempt to teach sound qualities, but I don't know of any ear training that attempts to teach musical concepts.
Last night, as I played Chordhopper and Interval Loader, I paid attention to how I was recognizing the sounds. I discovered that in every case, I was most easily able to identify sounds which represented a specific concept, and the ease and confidence of identification was directly associated with the uniqueness of the concept. In Chordhopper, I never fail to recognize the diamond (the "center triad"); I was perpetually confusing the ticket and the fish, though (F and G triads), until I realized that the ticket sounded like "Ob-La-Di", and now I rarely mistake them. In Interval Loader, I seem to have unconsciously picked out qualities which allow me to recognize the harmonic intervals and scale degrees; a few of these are melody-based-- such as "My Heart Belongs to Daddy" for the minor third or "Home on the Range" for the minor seventh-- and these never fail me, but others are quality-based-- such as the tritone's whine or the seventh's "pull" toward the tonic-- and these invariably fail when the context changes. That's the essential observation, perhaps directly parallel to word acquisition: the most effective concepts are the ones which are derived from some greater context, and the least effective are the ones which are inherent to the object and thus independent of context.
This would seem to suggest an outside-in approach to ear training. Rather than drilling pitches, intervals, and chords as though they were independently meaningful, perhaps a succession from melodies to progressions to chords would be the most conceptually effective process. Intervals and pitches would be learned for the purpose of "spelling" these "words", which could potentially allow those sounds to be learned not by their sound quality (weak concept) but by their musical function (strong concept). I suspect this accounts for the positive reports from users of "melody trigger" methods such as Modlobe or Pitch Paths, because melodies provide a strong-concept musical function; however, because the concept acquired is so firmly tied to a specific melody, the pitch knowledge gained by such a method is firmly associated with each training melody-- both as the initial tone and in a particular scale degree. I also wonder if the melody process is truly forming a musical concept.
Strong concepts for phonemes (and other non-word components) appear to be functional: you know what you can use them for. The syllable "di" has no (obvious) definition, but you know that you can use it for words like "dip" or "distance" and not for "pud". Right now I recognize a minor third from its use in "Daddy"; that is a concept, but it may not be a musical concept, because that melody is only one exemplar. I have an apparently functional understanding of the scale degree, because the concept is derived from a function, but my understanding doesn't actually serve any function because I can't use it for much more than the one melody. If, instead, I knew a minor third because it is the bottom interval of a minor triad, and I knew a minor triad because it forms the Nth part of such-and-such a progression... now that's useful. That would, potentially, allow me to understand an interval as a fully-integrated musical concept instead of a context-dependent sound quality or fixed-use exemplar.
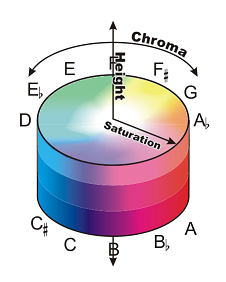
Is the pitch cylinder a two-dimensional surface or a three-dimensional solid?

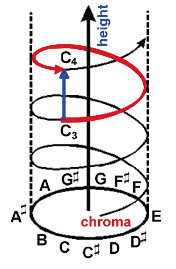
I've argued previously that the by-now famous "pitch helix" is in fact a one-dimensional model, because even though it cleverly twists around to visually represent octave equivalence, the "helix" is nonetheless a line, and a line is one-dimensional by mathematical definition. Thanks to the work of Griffiths and Patterson and their colleagues I've been able to represent the second dimension (shown by the blue line above) and travel along the surface of the cylinder, changing Y (height) without changing X (chroma). But if X is chroma and Y is height, what is Z?
It seems as though there should be a Z-dimension. If the pitch cylinder were truly a two-dimensional model, then presumably it could be visually represented without requiring an implicit third dimension. The pitch cylinder, in two dimensions, is evidently a hollow cylinder-- but the existence of a cylinder, rather than a plane, would seem to imply that something may occupy the "hollow" space, just as the existence of a helix, rather than a line, implied the existence of points between the turns (again, the blue line in the graphic). But the helix model was created because a simple line could not represent octave equivalence; likewise, a two-dimensional plane cannot represent octave equivalence either.
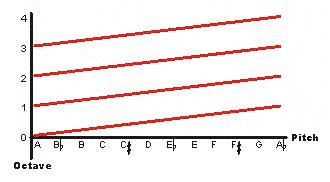
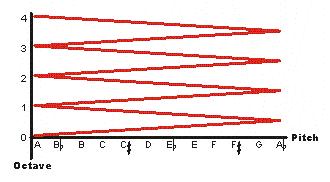
A broken line does not visually show the fact that a continually-ascending scale is in fact continuous, but a continuous line requires that a scale be simultaneously ascending and descending. Wrap-around suggests a third dimension.
So: how do you move along this line?
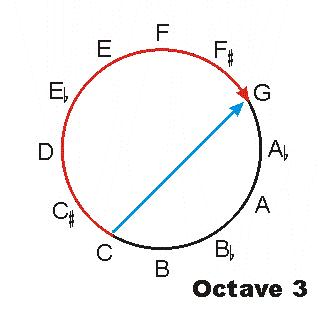
How do you move from C to G without passing through C#, D, Eb, E, F, and F#? What dimension of pitch is being changed?
What is the Z-dimension? X is chroma, the fundamental frequency of a tone, and it's easy enough to move from A4 to B4 to C#4 by increasing the frequency of a tone. Y is height, and once you accept that height is timbre you become able to move from A4 to A4.5 to A5 by attenuating (decreasing) the odd overtones of a tone. To allow movement from C4 to C/G4 to G4, pitch must possess a third quality. What could it be? How do you create "C/G4", a tone that is equally C and G and yet is not an interval, but a single pitch?
There is a theoretical model for this kind of movement: Mathieu's harmonic lattice.

Mathieu contends that this lattice is a legitimate scale-- a harmonic scale-- and he explains that movement along this lattice is accomplished through "compounding fifths and thirds." If you "go up" a fifth from C, you get G, without any other pitch classes in between. "Go down" a third from C and you're at A-flat. Conceptually, this does represent a movement across the circle rather than around it.
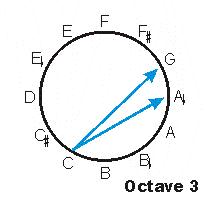
But how does this become continuous movement within the circle? Let's try the old reliable color analogy. How do you move within the color wheel?
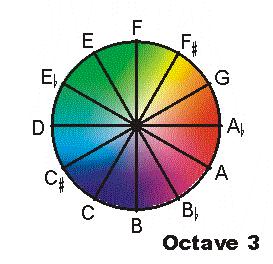
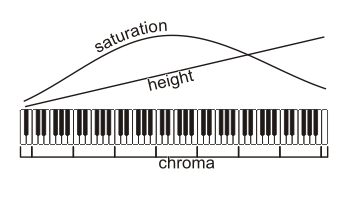
According to a quick look at color spaces, musical pitch space appears to most closely resemble the HSV color space, which is not actually a wheel but a bar. Hue (chroma) is represented by a single numeric value which may be adjusted by value (height) and saturation (volume?). This analogy isn't very useful, though, even if it is functionally appropriate, because the third dimension is not one which allows the fundamental color to change; you can't move from green into red by changing the saturation.
But HSV is the only model where hue/chroma has a single spectral value. All the other models-- RGB, CMYK, Lab-- arrive at chroma by intermingling "primary" components. RGB is a mixture of red, green, and blue; CMYK is cyan, magenta, yellow (and black); Lab is lightness plus values along the axes of magenta/green and blue/yellow. Could it be that there are "primary pitches" which allow the generation of any of the others?
The pitch circle can't be used exactly like a color wheel. If the CMY model were a direct parallel to the graphic above, then that would suggest by mixing 50% D, 50% B-flat, and 0% F-sharp, you'd hear a solid C. That's certainly not the case. And while you can mix equal parts C and G to achieve a sound that is not quite C and not quite G, according to color-wheel rules that should be an E, which it definitely isn't. I think Mathieu's lattice may explain why; on his lattice, E does not exist between C and G (nor does any other pitch). A mixed C/G sound would be just that: "C-G".
In this way, the color analogy is good for one more point. You may have listened to that C/G sound and thought that it sounded more like an interval than a single percept. Well, when you mix two colors such as red and orange you get a color that is neither red nor orange, but "red-orange". Its red properties and orange properties are individually apparent, if you look for them, but if you don't it looks like a single color.
This effect occurs normally in music, aside from the C/G pure tones I mixed together above. There's the opening of Clarence Clemons' "You're a Friend of Mine" (perfect fifth) and the opening of "Free to Be You and Me" (major third). It was only after I started using Interval Loader that I realized these opening sounds were not single pitches; as it is, I can let my mind flip back and forth to hear either the single percept or the individual pitches, just like I can look at the middle color above and see it as either "reddish" or "orangey" or a single color that's both-but-neither. But I'm not exactly suggesting that intervals are pitches.
It's not implausible to think that two or more frequencies could be mixed together to create a new sound that is a single pitch and not an interval or chord. I initially thought of the research which shows that a chord seems to have a single pitch value (Ekdahl & Boring 1934) or that any listener will be able to hear a single pitch in multispectral sound such as white noise (Patterson et al 2002, for example); I also combined an A4 with an E5 and, instead of a perfect fifth interval, found myself with a single A3 (here's a pure tone A3 for comparison). And then there's the overtone series of a complex tone, which is of course perceived as a single tone.
A complex tone already does have components that are other pitches. For example, here's a middle C that I just constructed. It's not a pure-tone 100% C; because of its overtones, this sound is 77% C, 16% G, and 7% E, but it does sound like a pitch and not a major triad. If I alter the mix, to give 50% C, 50% G, and 0% E, then it still sounds like a middle C, but it sounds like a different middle C-- one that's simply more G-like. Here are the two C's side-by-side. I'll try another one: 25% C, 25% G, 50% E. This is a third tone that is still middle C, but again, it's a different middle C which is less G-like and more E-like. Here are all three of them in sequence... and now just for comparison here's 5% C, 5% G, and 90% E, that no longer sounds like a middle C, but more like 100% E. Could this pitch mixing be movement within the Z-dimension?
According to Mathieu's lattice, it might be. Using a CEG mixture-- combining thirds and fifths, the way I've just done-- a pitch can move anywhere within this space.

This is among three pitch categories, yes, but in this space a tone can change its pitch sound without changing its pitch class (X-dimension) nor its pitch height (Y-dimension). If you listen again to the four different middle C's from the previous paragraph, you can probably imagine where they would be plotted in this space. This, the harmonic composition of a pitch, is potentially pointing toward a Z-dimension.
There is an immediate problem, however. For one, there are only three pitches here; how do you move out of this space to encompass the rest? And for another, how can this kind of Z-dimension be reconciled with a pitch cylinder, or even the pitch circle, if direct relationships between pitches are harmonic rather than scalar? Actually these seem to be the same problem; if it were possible to move out of this triangular space using only CEG components, then that would be equivalent to primary colors, and the direct harmonic relationships could be represented on the pitch circle in the same way that primary, secondary, and tertiary colors are represented on the color wheel. So there's the basic problem: moving out of this triangular space.
Perhaps, according to the lattice, we'd achieve secondary pitches by combining fifths and thirds. Adding a third to E and G, you get Ab and B, and adding a fifth to each you get B and D-- making the secondary pitches Ab, B, and D. But can CEG function as primary pitches like this? That is, can you "add a third" to E to actually make a recognizable A-flat pitch without actually using an A-flat? How do you "add a third" or "add a fifth", anyway? Mathematically, it can be done with simple ratio multiplication; can intervals be combined as easily as this? If so, how so? If I were a mathematician or a physicist the answer might be obvious... but I'm not, so it's not.
I guess I'll sleep on it.
I'm glad I took a break from the question of "primary pitches"; I looked a bit more closely at color spaces and found, at least in the short term, what seems to be a reasonable model of three-dimensional pitch space.
As I mentioned previously, conventional musical pitch space evidently resembles an HSV color space, where HSV stands for hue, saturation, and value. Hue is a single ordinal value which represents the color; this is directly parallel to musical chroma as a fundamental vibratory frequency. Value is a percentage, from 1 to 100%, which represents a color's brightness; this seems easily translated to tone height, even if only because studies have shown that naive listeners naturally select tones to be "brighter" and "darker" in correlation to "higher" and "lower". And then there's saturation, which is typically described as "intensity of color", but this "intensity" is not, as I had supposed, comparable to "volume" in sound. Saturation represents the purity of a color. Pure, saturated blue is 100% blue; unsaturated blue, like any other unsaturated color, becomes an undifferentiated neutral-- white, grey, or black, depending on the value.
HSV color space is not a linear spectrum, however, as I had initially thought. It is a wheel, with saturated colors at the rim and decreasing saturation toward the center; and, if you include value, the HSV wheel becomes... a cylinder. A solid cylinder.
So perhaps pitch can be defined in dimensions equivalent to HSV: chroma, height, and saturation.
Chroma is a sine wave-- a definitive fundamental vibratory frequency. This is the rim of the pitch circle. It's a pure tone, an unadulterated chroma with no other interfering sounds.
Height is a mathematical average of the power spectrum, measured against the entire range of audible sound. Height is best illustrated with noise. Noise has no fundamental frequency, but it still has a perceptible "height" depending on where the power spectrum is most heavily weighted.
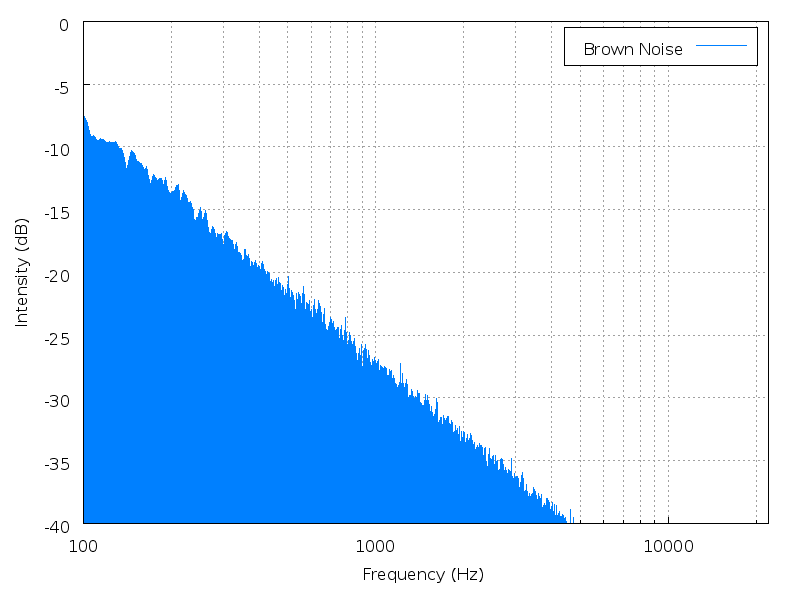 |
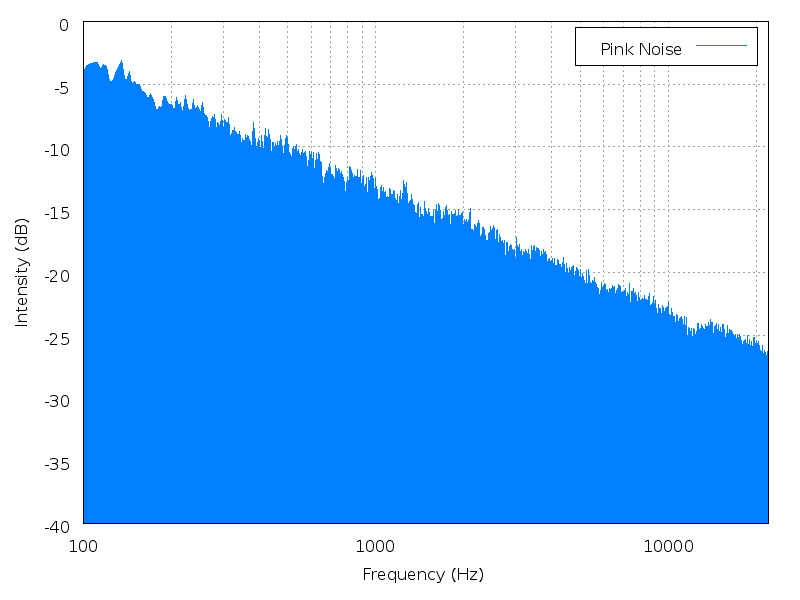 |
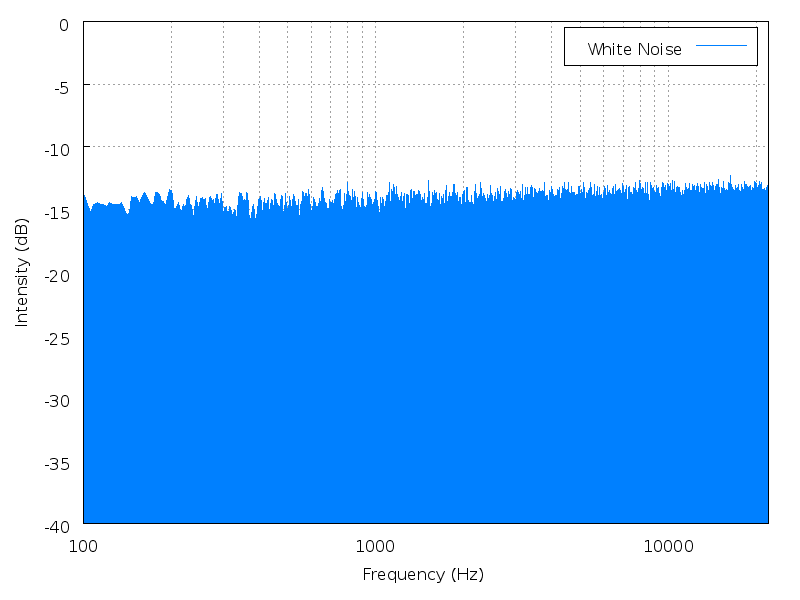 |
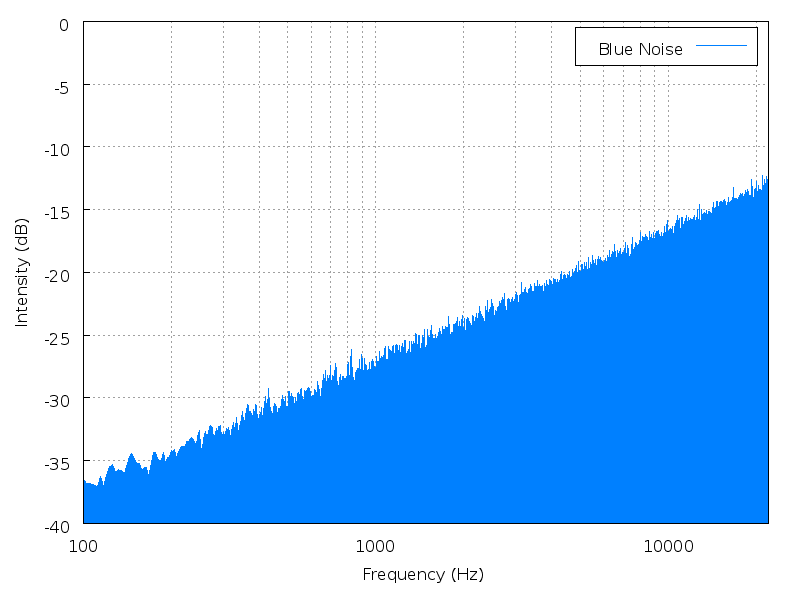 |
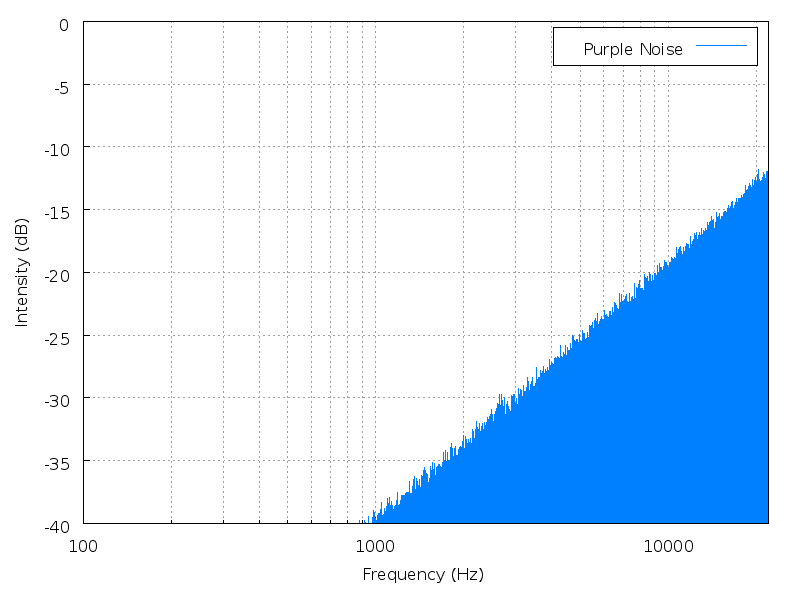 |
| Brown noise | Pink noise | White noise | Blue noise | Purple noise |
Click an image to enlarge it; click its name to hear the
sound.
(images and sounds borrowed from Wikipedia
colors of noise)
This is a better definition, I think, than "height = timbre". A pure tone has no overtonal timbre, but by this definition it must possess height simply by occupying a position within the auditory spectrum.
Saturation, then, may be a qualtitative evaluation of the power spectrum. Where height is an objective function versus the entire range of sound, saturation could be a measure of how an overtone series emphasizes or obscures its fundamental chroma. Not only would this saturation dimension not require "primary pitches", but as a description of the overtone series it could potentially include any of the twelve pitch classes in any proportion-- from their complete absence in the fully-saturated pure tone to their overwhelming presence in neutral white noise.
Saturation isn't height, and it isn't chroma, but it's certainly recognized and mentally synthesized as a characteristic of a single tone. You might describe it as measuring the "visibility" of chroma within a tone. Eric, in the forum, provided a document which graphs the power spectra of various instruments; look over the document and consider the graphs to be illustrating the instruments' pitch saturation levels. The bagpipe, for example, is described:
There is a strong prominence of odd harmonics... the third harmonic (second overtone) is especially strong, exceeding all other mode frequencies in power. Not only is the third harmonic more powerful than the fundamental frequency, it appears to have more power than all the other modes combined. This gives the bagpipe its characteristic harshness.
In other words, the "characteristic harshness" is a desaturation of the fundamental pitch. Violin, by comparison, produces a more saturated sound.
Note the dominance of the fundamental frequency. The most powerful overtone is the first, but only slightly more than 10% of the total power. The higher overtones produce much less power. Of the higher overtones, only the second overtone produces more than 1% of the total power. The result is a very simple waveform and the characteristically pure sound associated with the violin.
Saturation, by this definition, seems almost common sense. Think of the range of a piano; compare it to the HSV cylinder and your intuitive understanding of color. The lower height is "darker" to begin with, and the tone is desaturated ("muddied") by the wider, more variable overtone series; together these factors make it more difficult to detect its chroma, and this seems similar to how it's difficult to recognize an extremely dark color regardless of its hue. On the other end, an extremely high tone has a "lighter" sound and, although presumably more saturated due to the inaudibility of the dissonant overtones, less detectable because it lacks the presence of more consonant overtones. In fact, now that I consider it, a 100% saturated tone would likely not be a single sine wave, but sine waves of the same chroma with equal power in every octave, sort of like a Shepard tone-- as a combination of eight pure-tone C waves from all eight octaves of the piano, it could sound sort of like this.
This model would produce an acceptable three-dimensional cylinder, with saturated tones at the rim, "white noise" at the center, and height running from top to bottom (as light to dark).
I suppose this could be another way to look at it:
Now that I'm more aware of the topic, I see that there is plenty of study on tonal pitch space, pitch space, pitch class space, and it all dates back as far as the 1800s. I'm not yet sure, of course, how my little mental fling here will fit in with the centuries of study; I get the impression that Patterson et al's infinite height and my own suggestion of "saturation" will probably be already observed and studied in various ways, but that the model of "two-dimensional" tones will be essentially adhered to, with other attributes of sound considered not to be aspects of "pitch".
Last week I was preparing a sandwich in the kitchen and I suddenly recognized a familiar scent. I knew I'd smelled it before, and I thought I remembered from what, but I couldn't be sure-- because even though I could recall the object I thought had been the cause, I couldn't remember its odor. I couldn't match my current sensory experience with a sense memory because the sense memory doesn't exist.
Thanks to lifelong allergies, I can rarely breathe easily through my nose; my sense of smell is usually "turned off". Smell is not part of my experience of the environment; to me the sense only kicks in occasionally, to notice that a particular object has a particularly strong scent. My sense of smell works; I can perceive a smell and describe what it's like, and I can also identify definitive scents for what they are (bread, coffee, sewage, gasoline), but unless there is an odor lingering in the air for me to directly perceive, my olfactory sense is stubbornly absent. There is no place in my brain which can imagine a smell.
So it is evidently possible to exactly recognize a sensory input without being able to recall it. Does this explain "passive" absolute pitch-- the observed phenomenon in which people are able to recognize pitches perfectly well but can't reliably produce them upon demand? I don't know for sure that my physical experience of smell is responsible for its neurological absence, but I can certainly imagine a similar situation for a musician. Their pitch sense may be "turned off" in their everyday experience of music, but they could nonetheless passively learn to recognize certain pitch identities-- such as their instrument's strings-- as meaningful and definitive.
If this hypothetical musician had no memory store for remembering a pitch sound, then perhaps he is neurologically unable to learn absolute pitch? If this were possible, if this is indeed what happens in all normal (non-absolute) musical development, then no amount of training could possibly get anyone beyond the ability to recognize individual pitches in isolation. I'll tell you, though, what makes me think that this is not the case, if you do this right now:
Imagine a single tone. Just one tone, from any instrument.
Did you "hear" anything? Most likely you did. This is, I think, what makes the difference. When I try to imagine a smell, I get nothing at all. I don't have a weak or imprecise memory; it's a complete blank. The fact that you can imagine a single tone would seem to suggest that the memory facility for pitch sound is present-- in which case it's the interpretation of that memory which makes the difference.
It would seem, then, that the basic question is not "can absolute pitch be learned?" but "can people learn to interpret pitch differently?" This is the premise underlying Absolute Pitch Blaster's perceptual-differentiation approach; theoretically, perceptual differentiation training will force a person to zero in on chroma. However, I've realized that there must be other steps because, when adults become able to separate out the sound of the fundamental frequency, they do not automatically recognize chroma quality. Instead, they learn to quantify "areas" of the spectrum.
Researchers typically assume that "pitch area" is an absolute pitch strategy. Because absolute judgment is "drawn from a sensory continuum" (Siegel & Siegel, 1974), they reason, someone with absolute pitch ability must have learned to recognize bounded areas of that continuum. Therefore, when training and testing for absolute pitch, answers that are "nearer" to the target are more accurate than answers that are "further"; errors of one or two semitones are near misses and essentially correct. Indeed, this is how Brady (1970) explicitly evaluated himself; in his final testing he only gave 65% correct answers, but he lumped in his 31.5% semitone errors and claimed 96.5% overall accuracy. However, as Bachem observed in 1937, semitone errors do not typically appear in true absolute listening except "in the outer ranges of the scale" as chroma fixation begins to creep in (Bachem 1948). Absolute listeners make octave errors, said Bachem, while non-absolute listeners make semitone errors. Bachem further explained that although the non-absolute listener's error size can be reduced by training ("to 4 or 6 half-tones"), their strategy is still based on height.
Semitone errors are a measure of height accuracy, not chroma, but they nonetheless seem to be a popular measure of absolute pitch training success. You can see in the "Finding the Special Note" chart how adults gradually narrow their answers inward toward a target, making increasingly accurate absolute judgments, and though the researchers acknowledge that their subjects are using an "area" based strategy they still seem to be improving in their absolute judgment. The "Special Note" training is perceptual differentiation, and would thus imply that its subjects would learn to hear chroma; but it is possible to make an absolute judgment of "chroma" height. Presented as a sine wave, A220 is still "lower" than A440, and it occupies a precise "area" of the spectrum where it can be absolutely located.
It's not enough to become able to hear and recognize chroma as a characteristic. People must be trained to evaluate chroma sensation not as a location on the auditory spectrum but as a member of the pitch circle. Chroma possesses no physical location and, as an alphabet, stands in an order determined more by convention than perception. It seems to me that until a listener learns to identify chroma based on pitch category rather than height "area", they will never learn absolute pitch.
If it's possible to move vertically by varying height without changing chroma, shouldn't it be possible to vary chroma without changing height? How do you go around the perimeter of the pitch circle without getting "higher" and "lower"? How do you follow this red line without going "up"?
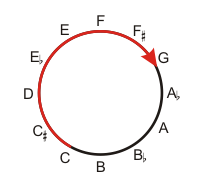
Changing height should be simple. If "height" is a mathematical average of a tone's harmonics, then it should be possible to use only two sine waves to create a C4.5 (here's C4/4.5/5 for comparison). And then the same two sine waves should be adjustable to create quarter-height tones, so you can have C4, 4.25, 4.5, 4.75, and C5 in an ascending series. If you're a trained musician you'll probably find it difficult to integrate these sounds; you may hear these tones as becoming "brighter" rather than "higher".
And if height can be the mathematical average of only two sine waves, then it should be possible to take any two sine waves and adjust their power to create any height between them. For example, equal parts C4 and C5 average to 392.44Hz; that's the same as G4 (392.00Hz). Mathematically, they're the same height, but I still hear a C4.5-G4 as an ascending interval. I made a series of 12 two-wave tones, using all 12 pitch classes, which all averaged to 392Hz plus or minus 1.5Hz (the just-noticeable difference); but again, even though these tones were now mathematically identical, I distinctly heard an ascending scale. Drat!
However, I soon discovered I had inadvertently re-created a two-component Shepard tone series. I hadn't realized that Shepard tones are not merely "octave chords" as I had thought, but that the overall spectral envelope is held constant regardless of the pitch class, so that the mathematical average of each tone is the same. Shepard tones are indeed all the same height.
But how can this be? If these tones are all identical in height, if they do in fact go around the pitch circle without going up or down, why would they appear to ascend or descend at all? Diana Deutsch and others have said that this effect means pitch classes have inherent height value, and the fact that we are able to make a height judgment based on pitch class alone means that the general population actually has absolute pitch ability (albeit unconsciously). I would agree that the Shepard tones (and Deutsch's tritone illusion) reveal that even the most naive listener is aware of and able to detect pitch chroma categories-- but I would offer a different conclusion. I think that the Shepard tones unambiguously show that the general population can hear chroma, but even when they do hear chroma they will misinterpret chroma as height.
Here's an example using two-wave sounds. This first pair of tones is G4.75 followed by A3.8. If you listen to this tone pair without any expectations, your mind will probably make a height judgment (685Hz vs 392Hz) and you will most likely hear a descending minor seventh. But if you listen to G4 and A3.8, which are both the same height (392Hz), you will hear an ascending whole tone; then when you listen to the pairs together (G4, A3.8, G4.75, A3.8) the true fundamental of the G4.75 kicks in and you will probably hear the third and fourth tones as major seconds rather than minor sevenths. If you do, then this demonstrates essentially what Shepard and his followers have asserted, which is that you really are hearing the chroma independently of the height; and when you listen to chroma, tone height does not disappear but becomes a separate, irrelevant timbral quality (so perhaps you can hear, in this example, why absolute listeners so easily make octave errors). And yet, even when you are listening to the chroma quality of the tones, you are still hearing steps that go "up" and "down". [It should be possible for anyone to make themselves hear these examples the way I'm describing them-- but musicians may find it difficult to make themselves hear the first pair as descending, and non-musicians may have great trouble hearing the third tone going down instead of up.]
I've been told, personally, by more than one absolute musician, that "tones are not 'higher' or 'lower'; they're just different." The research shows the labels of "high" and "low" are an arbitrary convention which people gradually learn to accept regardless of their musical experience. What if a person learned to judge pitch classes according to a metaphor other than "height"? The ascending Shepard tone mystery would be solved immediately, because the tones would no longer seem to be an ascending scale but going around a flat circle instead, all at the same height, changing only in this other cyclical quality.
I'm not suggesting that absolute listeners don't hear a relationship between neighboring chroma, or that they can't hear pitch chromas as higher or lower than each other. I think that chroma does possess a quality of height; but to an absolute listener height is a secondary quality of chroma, while to a normal listener height is the only quality.
I'll try an analogy to show what I mean. These colors are all the same brightness.
![]()
And yet, if you compare any two of these squares, one will very probably seem immediately "brighter" to you. It's more obvious when you look at the "bright" and "dark" patches of the full spectrum (still all at the same brightness).
![]()
Brightness is a characteristic which could describe each of these colors, but brightness is not a definitive quality you're using to recognize or identify any of them, and brightness is not the most meaningful way to compare the colors to each other. When you look at the spectrum (or the boxes) your mind can accept that they are exactly the same brightness even though they are obviously all different color categories. Brightness and color are qualitatively separate attributes.
I set up this analogy just to be able to construct a parallel sentence describing how absolute listeners may perceive the Shepard tones as a flat circle:
Height is a characteristic which could describe each of these pitches, but height is not a definitive quality you're using to recognize or identify any of them, and height is not the most meaningful way to compare the pitches to each other. When you listen to the pitch circle (and the Shepard tones) your mind can accept that they are exactly the same height even though they are obviously all different pitch categories. Height and pitch are qualitatively separate attributes.
But as the Shepard tones demonstrate, chroma has apparent "height" separate from tonal height, and this is the strategy we will use. No matter what method we employ to learn to detect chroma, once we learn to detect chroma we will evaluate it by its height and position on the pitch circle. Compare this to the color spectrum; how often have you had to use the mnemonic ROY G BIV just to remember which colors are supposed to be next to each other? In true absolute judgment, proximity and relationship are secondary factors or even afterthoughts.
What I'm simultaneously dancing around and leading up to is that absolute pitch ability is not based on tone chroma. I've been convinced for some while now that note-naming is a symptom of absolute pitch rather than its definitive aspect, and yet I had no other explanations, so I had accepted that "identifying chroma" was making a judgment of the fundamental frequency of a musical tone. The logical and obvious consequence of this assumption is that if a person can learn to recognize and identify the chroma of a musical tone, without "using a reference tone", they will be able to learn absolute pitch. The aural sensation and labeling judgment of a single pitch frequency is assumed to be the goal, the target, the Grail of absolute pitch judgment. But it's not. It hardly seems that it could be-- because it can't explain all the abilities correlated with absolute pitch, for one, but more importantly, because a single characteristic does not represent an object. Bergan (1965) says it well, I think (with my emphasis added).
[A] continuum may be imagined, one extreme of which would be an auditory image, the other the absence of such an image. As more and more qualities were subtracted from the image, it would tend to stand less and less for a particular sound and in this respect become more general or abstract. Such an abstraction, in the case of a simple musical sound, would be a perception which could stand for any tone. This does not imply that a perception of this sort would be identical with the concept of tone, but rather that such an experience would be abstract in the sense of being indistinct. Thus, for example, a tone might be thought of as involving a certain frequency, a certain source, a certain intensity, a certain timbre, a certain placement, a certain clarity, a certain relationship to volition in term of the amount of perceived participation in making the image come about, and finally, a certain degree of belief in the reality of the sound. ...The absence of definite quality in any one of these areas would tend to make the perception less distinctive and consequently more general or abstract. The absence of all of the characteristics would suggest forgetting.
Bergan's paper observes a strong correlation between pitch naming skill and the vividness of a person's imagination. Absolute pitch, then, may not be the ability to recognize tone chroma and categorize it by pitch class, but an ability to conceptualize a certain musical characteristic which is most abstractly expressed by (by, not as!) the fundamental frequency of a musical tone. The same characteristic, in various forms, guises, and influences, is undoubtedly an observable aspect of other "musical images" as well-- at the very least, tones in other octaves and the key signature of a composition-- and the absolute listener would recognize that quality not because of a template of pitches and notes and frequencies but by their capacity to clearly imagine this abstract quality.
This supposition appears to be supported by some work by Hiroyuki Hirose and his collaborators. They found in 2005 that absolute listeners, when listening to tones, show a significant increase in right-brain activity where non-absolute listeners do not; Hirose et al speculated that this right-brain activity means that "adults with [absolute pitch] have developed the ability to analyze [the tones] in the right hemisphere and assign names to the tones in the left hemisphere." Their results are supported by the current work of Gutschalk and Patterson who have been consistently demonstrating that pitch recognition is not a direct perception but a temporal analysis-- which is in turn supported by Fujisaki and Kashino (2005) who showed that absolute judgments are best drawn from analysis of temporal configuration, while relative height judgments are best drawn from absolute frequency.
Which means, I'm pleased to say, that Absolute Pitch Blaster is doing more than I thought it was. The game places a tone in structures of increasing complexity, which I had figured would accomplish perceptual differentiation and strip away everything that wasn't chroma; but also, it seems that increasing complexity also forces a listener to engage a temporal analysis rather than a place recognition which makes chroma still easier to hear. Nonetheless, while Absolute Pitch Blaster may (for these reasons) be the first-ever method to teach even non-musical students how to extract and evaluate tone chroma (such as the people who can't hear the third note as descending no matter how hard they try, as this requires chroma extraction to succeed), that's only a first step. It's still necessary to learn how to judge that chroma as something other than height, and to gain the ability to imagine chroma as a unique abstract quality.
How can this new ability be trained? How can the concept be formed, and furthermore divided into categories? Rob Goldstone provides a hint.
For this measure, emphasizing features shared by category members may be more powerful than emphasizing features that distinguish between categories because participants are likely to form complete images for each of the two categories. Previous work has suggested that when image-like concept representations are encouraged, concepts tend to be represented in terms of their within-category commonalities rather than the features that distinguish them from other categories. Once properties shared by the members of a category have been emphasized, these properties will bring representations for members of the same category closer together. (Goldstone, 2001 - see Phase 14 for citation)
Fujisaki and Kashino (2005) seem to think this is the way to go.
Children who pay more attention to temporal cues than to place cues and learn the connection between temporal cues and note names may acquire AP. The tendency to use temporal cues for identifying chroma may be enhanced if teachers put a stronger emphasis on chromatic structures than on the absolute height of musical pitch when they teach note names at the early stages of children’s music experience.
What are the chromatic structures which are the pitch-class category members whose shared features can be emphasized? Beyond the multiple octaves of a single tone, I can think of a handful right off the bat-- intervals and chords with the pitch root, chord progressions which evoke the pitch key-signature without containing it, and the key signature of a melody. Key signature does seem singularly important. A musical composition conveys its key feeling (and therefore chroma) throughout, even though its actual tonic note is played only occasionally; and Grebelnik in his method said that the best way to teach absolute pitch to preschoolers was to help them make the connection between pitch, interval, and key signature (the Russian version is on-line as is my inexact English translation).
I think it's possible to go further. A musician with better knowledge of music theory could probably come up with many more category members-- and nobody else is yet thinking of training absolute pitch as musical literacy.
I think I understand now what needs to be done to learn perfect pitch; I don't yet know exactly how to do it all. My strategy and perspective is drawn directly from my understanding of learning language as an adult-- or even as a child. The approach must be two-sided, with a holistic perspective and a linguistic twist. On the component side, it's necessary to learn the pitches, intervals, and chord sounds individually and independently. On the comprehension side, it's essential to engage in musical communication-- both interpreting others' statements and formulating one's own musical expressions. Once you know how to comprehend a musical idea, you can encode your own or decode others' using your component knowledge. The two sides grow to meet each other through encoding and decoding; the part I haven't yet licked is figuring out how to create and impress a comprehension of musical sound separate from the sound's raw physical attributes.
By a "holistic perspective" I mean to emphasize that the entire purpose of the endeavor is to enable musical communication, which I define as the creation, expression, and reception of musical ideas.
How do you create a musical idea? It's easier than you think: Keep your mouth closed, keep your body and hands still, and try to talk to someone. You have to actually make them understand you, unambiguously, without their having to guess or read your mind. You'll probably want to avoid speaking words in your head, or gesturing indicatively; as Diana Deutsch's Track 22 demonstrates, our consciousness normally gives exclusive priority to language sound, and only by disallowing both language and gesture (through habituation or suppression) will your musical message become immediately purposeful and objectively meaningful. If you try this exercise, and focus on producing meaningful communication, you'll very quickly learn what you can and can't "get across" with only musical sounds. In trying this exercise, you'll discover that formulating a musical idea is a simple and natural process which you do unconsciously all the time, and "composing" that musical idea into explicit sound is instinctive-- and ridiculously easy. Over time, attending to your own natural compositions will help you to develop increasingly complex musical ideas.
It's easy to see, then, how learning the components of music would allow anyone to write down their musical ideas-- and the more familiar you become with the components, the more effortlessly you can encode your ideas into written language. I agree with this author's statement of the problem: "[learning to read and write] does not involve learning a language but a code expressing a familiar language."
This is what I mean by a "two-sided" approach to learning. Comprehension and component are developed simultaneously, gradually come together, and continue to inform each other as overall literacy grows. I agree with this article's argument for why both sides are necessary:
[T]he debate that has occurred over these two positions [phonics and whole language] is an artificial one... No matter how bright, creative, and knowledgeable about oral language and the world a child may be, he or she cannot read and write well unless the code of written English is known. No matter how well the code is known, a child will not want to read or write well unless the child has been under the spell of a wonderful story or seen the value of communicating in writing.
Learning to receive musical ideas might not be as simple. Creating a musical idea is a natural process; you have a meaningful notion pre-formed and learn to assemble components to give voice to your idea. Both sides are plainly obvious. With reception, however, meaning can be completely disregarded. Written meaning can be totally lost if the reader mechanically reproduces components received from the page; audible meaning can be misheard as vague physical sound events with no actual information being transmitted. You can be "under the spell" of a wonderful piece of music and have no idea why. For a person to receive a musical idea, that person must be made aware that there is an idea to be perceived, made to comprehend the nature of a musical idea, and made to understand how the sounds represent those ideas.
That last part seems the most crucial: hearing musical sounds as representative symbols rather than physical events. For example: Why would "frequency ratios" have anything to do with musical intervals?
It's true that an interval can be described, literally, by a ratio of vibratory frequencies. If you take A440 and pair it with E660, that's a perfect fifth; 660/440 = 3/2. This ratio is a physical event, in that a signal of 660Hz will "beat" three times for every two beats from a 440Hz signal. It would seem logical to assume, and easy to test, that any frequencies which beat three-to-two will also sound like a perfect fifth; sure enough, yes, they will. But while all 3/2 ratios are perfect fifths, all perfect fifths are not 3/2 ratios. In equal temperament, E is not 660. E is 659.2552, and 659.2552/440 is 442/295. Not 3/2. Not a "perfect fifth" ratio.
How can 442/295 be a consonant fifth? Conventional wisdom and accepted practice seems to indicate that "simple" ratios are consonant and "complex" ratios are dissonant. Simple is usually defined as "low" integers such as 3/2, and complex is usually defined as "high" integers such as 40/27... but if that were the case, the high numbers 442/295 would surely be a hideously dissonant interval, instead of the essentially consonant equal-tempered fifth. Even 529/346 sounds like a slightly sharp fifth, still consonant as can be.
Why is a mistuned interval, with a mathematically different ratio, heard as "sharp" or "flat" instead of a completely different interval?
It seems likely that this perception is yet another way that intervals are like vowels. Vowels are literally intervals-- an interaction of two sound frequencies.
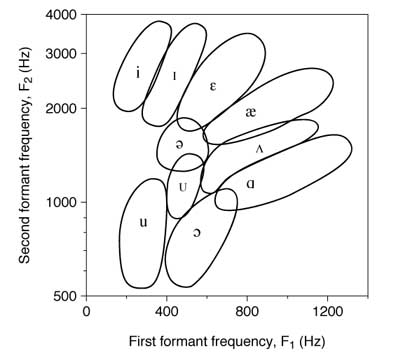
Any given vowel exists within a range, and so do intervals. If two frequencies fall together within one of the ranges on this chart, the result will be perceptually integrated into one of the vowel categories; musical intervals also span a range of interactions, and any pair of frequencies can be perceptually assimilated into the nearest interval category. 442:295 and 529:346 may be terrible fractions, but they make fine decimals: 1.498 and 1.529 are almost 1.5, or 3/2, and will be perceived as major fifths.
Are vowels and intervals actually the same categories as each other? A recent paper claims that they are, saying that the musical scale is what it is because each interval can be matched to a vowel. It's a pretty idea, and an appealing one. 650/325, or 2/1: octave or oo vowel? 1100/880, or 5/4: major third or ah vowel? But that's too simplistic. To begin with, the categorical vowel boundaries span multiple intervals; 1400/1200 is also an ah vowel by this chart but 7/6 is a minor third, not major. Then, beyond the theoretical mathematics, I constructed a musical scale from vowels years ago and received enough feedback to know that different people's vowels will match different intervals. Vowels and intervals are not the same.
Yet if intervals aren't vowels, why should there be interval categories at all? Intervals are produced by specific physical harmonic interactions. Vowel sounds are referents of abstract concepts, while interval sounds are concrete images of the physical motions which generated them. Or... are they?
Since finishing Phase 14, I have done more work with the trichord experiment; I've run more subjects and found new ways to analyze the data. One of the more important results of this new analysis is that categorical perception of intervals is clearly present, in a statistically significant way, but only for trained musicians.
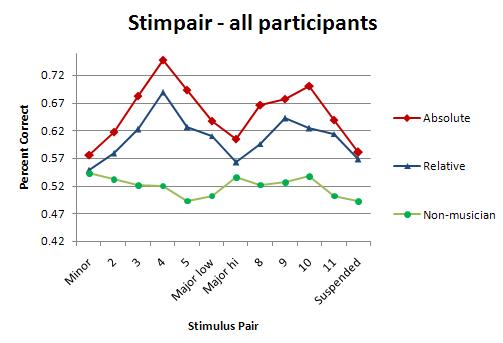
The peaks and valleys of this chart represent the fact that trained musicians heard intervals as their respective categories (minor third, major third, perfect fourth); the flat line represents the fact that non-musicians didn't. In the context of the current discussion, the result could mean that musicians have been trained to hear musical interactions as "referents of abstract concepts" while non-musicians, indifferent to category, hear "concrete images of the physical motions".
The data show that the more experienced a musician is, and the more able they are to abstractly analyze musical sound, the less influenced they are by the physical properties of music. Since the chart I've just shown you is for intervals, I was about to show you that a chart of pitch categories would show that relative musicians have a flat line while absolute musicians show the same peak-and-valley categorical response, but to my surprise I just discovered that there aren't any papers which show this. There are a handful which show absolute musicians' categorical response to pitch, but these same papers don't show the relative musicians' lack of it. I suppose they assume, as I am assuming, that relative musicians' judgment of pitch would indeed produce a flat line, like the non-musicians' judgment of interval above.
I reiterate what I take this to mean: trained musicians learn to interpret musical sounds not as physical events, but as tokens of abstract concepts.
I'll show you what I mean. Say the vowel "oo" as in boot and the vowel "ee" as in beet. Between these two vowels, the musical interval is substantially wider, but do you even notice? The second frequency in ee is about two octaves higher than oo, but does that fact even register? No, not at all. If you really force yourself to listen to the physical sounds-- willfully disregarding the linguistic value-- you might be able to perceive the differences in "height" or "width" between these vowels' frequencies... but not easily. The sounds' shared physical properties are thoroughly subsumed by the unique concepts they represent.
I'll repeat that, as well: trained listeners judge a sound by its symbolic meaning rather than its physical properties. Once a sound is comprehended as a symbol, its auditory characteristics are mere curiosities (if they are perceived at all). This extends beyond language or music-- after all, if you hear dishes breaking and silverware clattering to the floor, you don't try to capture an impression of the raw sound and attempt to analyze its physical characteristics to figure out what you've just heard; you recognize the sounds immediately and objectively because of what you know them to represent.
Playing Chordhopper, I've learned to recognize some chords symbolically. There are three pairs of chords which sound very similar to each other: ticket/fish, flower/raindrop, and basketball/marble. The chord pairs have the same structure as each other (respectively root, first inversion, and second inversion) and are transposed by only one tone (orange = F or blue = G).

The strategy most obvious to anyone is to analyze the physical "height" of the chords. After all, in each pair, orange is always lower and blue higher. However, all the chords at the top of this square are relatively "low"; when you hear a series of low chords you can easily tell which are higher and lower within that low area, but as soon as that series is broken with a high chord, you're reduced to guessing whether it's the high-low or high-high chord (and vice versa from a series of high chords). While I was reliant on the "height" strategy I couldn't progress any further in the game.
Then, for no reason, I suddenly realized-- hey, the orange ticket sounds like the first chord in the Beatles' Ob-La-Di. Immediately I stopped confusing the ticket/fish pair; one was Ob-La-Di, and the other wasn't, and that's all there was to it. The next to reveal itself was the basketball, just a couple days ago, as it spontaneously occurred to me this was the opening chord of "My Country 'Tis of Thee". Just as quickly I stopped confusing it with the marble.
The solution isn't to match every chord to a song, though, and that's not how the flower/raindrop problem was solved. Once I could easily distinguish between these first two pairs, I was surprised to find that I could already tell apart the final pair, because the flower "belonged" with the orange chords and the raindrop "belonged" with the blue. The same-colored chords all have the same components, in different inversions (F-A-C or G-B-D) so they certainly should belong together, but it's curious that the shared quality has begun to appear as the orange category or the blue category. Curious-- and vitally important. I seem to be forming unique abstract categories for each root chroma. I'm no longer trying to analyze characteristics of the chords; not high-low, for sure, and I also don't have to try to feel qualities like "sharp" or "dull" or "thin" or any other subjective analysis of the physical sensation. Consequently, I'm flying through my current sessions with almost 100% accuracy, and the only thing holding me back is the fact that I still need twelve more flies to hit the game's next level.
Also, in each Chordhopper session, the A-flat stands out symbolically when I am identifying single pitches. I can get almost all of the pitches correct anyway, but this is because of associations with Melody Words or an occasional relative judgment. When that A-flat appears, though, it just is. I was startled in one session when I heard a C followed by an A-flat and discovered that, while I knew and could hear that this was a minor sixth, it felt as though the A-flat was actively rejecting its relationship to C and the C-major scale in favor of its A-flat pitch identity.
Because of how I hear A-flat and Chordhopper's emerging color categories, I believe I understand absolute musicians' assertion that pitches do not have height. This is also why I agree with Fletcher who does not consider a semitone error to be "almost correct". The vowels oo and ee are physically "higher" or "lower" than each other, but that's irrelevant. Hearing eh and calling it ih is "almost correct" if your goal is to compare physical sounds-- mathematically, spectrally, they're right next to each other-- but if you're trying to identify a vowel it's just a wrong answer. The same principles (and standards) apply to categorical perception of musical components. The absolute-pitch training results of a person like Brady (1970), who "achieved a performance level of 65% exactly correct and 97% correct within [a semitone]", are meaningless, because he is attempting to mentally measure the magnitude of a shared physical property-- namely, tone height. He is not using a categorical strategy of recognizing symbolic tokens.
To achieve musical ability, whether relative or absolute, one's recognition strategies must be changed from physical to symbolic. Until chroma is categorically, symbolically, objectively recognized, labeling pitches is still a physical height estimate, not absolute listening.
How can symbolic pitch recognition be induced? I think I can figure this out, even though I have not yet learned why A-flat is symbolic for me and the other eleven tones aren't (it changed spontaneously, without any special or additional training). The "orange" and "blue" categories developing in Chordhopper must certainly be F and G. I think what's happening there may be described by one of Robert Goldstone's papers, which suggests that making "different" judgments draws attention to individual characteristics and making "same" judgments draws attention to shared features. Absolute Pitch Blaster enforces "different" judgments by perceptual differentiation, which isolates pitch chroma. Perhaps "same" judgments will develop the necessary categorical-symbolic perception of that chroma. I suspect I'm unconsciously making "same" judgments in Chordhopper; in deciding between orange and blue I'm drawing attention to the unique perceptual quality present within each category, and if I can make that happen on purpose-- using, perhaps, not only single tones and chord roots but tonality as well-- then I should be able to make anyone learn absolute tones and true absolute listening.
But this skill, alone, will still not be musically useful. Despite my symbolic representation of A-flat and of all 12 harmonic scale degrees, I still struggle and fail to apply this knowledge when I'm listening to music. The harder step, the larger step, which I don't yet know how to approach, is how to train a listener to accept and interpret entire compositions-- complete musical structures-- as symbolic transmission of information rather than physical sensory experience.
I think I've done Jenny Saffran a disservice.
At the very least, I've learned that there's a difference between what the major media report about a scientific study versus what's actually in that study. Most recently, many of you may have seen the article from UCSF; the popular press reports on this paper as "proving" the genetic origin of absolute pitch, when of course it does no such thing. The article merely points out that people tend to be able to name every note or none at all, and very few people can sort-of do it. This "have it or don't" is what the researchers think points to a genetic on/off switch-- and yet, anyone could argue that note-naming is merely a manifestation of a wider ability, and furthermore that a critical period of development could be responsible for the have-it-or-don't; so this article doesn't prove nor even demonstrate much of anything.
When I initially took a look at Saffran's publication, the media had been gushing over it ("infants proven to have absolute pitch!") and I misattributed that claim-- I mistakenly thought that the media had accurately represented the purpose of her paper. Even though I quickly found that her paper made no direct claim about infants "having" absolute pitch, I was entirely confused by the "tone words" which she described, and without understanding that the "tone words" had been designed as an outgrowth of her previous research I inferred that she had done some unusually complicated thing to artificially wrangle an apparent, and illusory, result. Now that I take another look at her paper I find that I still disagree with her result, but for a different reason, because now I actually understand what she was trying to do.
My missing piece was her work on linguistic segmentation. She began with this experiment:
24 8-month-old infants from an American-English language environment were familiarized with 2 min of a continuous speech stream consisting of four three-syllable nonsense words (hereafter, "words") repeated in random order. The speech stream was generated by a speech synthesizer in a monotone female voice at a rate of 270 syllables per minute (180 words in total). The synthesizer provided no acoustic information about word boundaries, resulting in a continuous stream of coarticulated consonant-vowel syllables, with no pauses, stress differences, or any other acoustic or prosodic cues to word boundaries. A sample of the speech stream is the orthographic string bidakupadotigolabubidaku. The only cues to word boundaries were the transitional probabilities between syllable pairs, which were higher within words (1.0 in all cases, for example, bida) than between words (0.33 in all cases, for example, kupa).
She discovered that infants exposed to these syllabic streams would automatically infer that bidaku belongs together and gopada does not. Even though all the syllables of each "word" had appeared at various times in the stream, they only appeared in these patterns, and the infants detected this.
Her next logical step was to try it with music, and this is where the "tone words" came from. If you replace the English syllables with musical pitches, you end up with "nonsense words" made out of three tones each-- one tone per syllable-- which can be presented in melodic musical streams. Doing this, she discovered that adults and children picked out the patterns with reasonable accuracy, recognizing which three-tone sequences were "words" and which were not.
So Saffran naturally wanted to know: are these patterns being recognized as absolute tones or as relative intervals? This is where she got so tricky that, since I did not originally know the origin of her "tone word", I couldn't understand what she had done. I'm still not a hundred percent certain, but I believe this is the deal: she presented the pitches so that the intervals formed between certain words were the same intervals as were within other words. If, for example, you had the four "words" CEG (M3 + m3), CDE (M2 + M2), DGA (P4 + M2), and BF#A (P5 + m3), then by putting together the two legitimate words DGA + BF#A you would create an M2 + M2 in the middle of them. If you were listening to the absolute tones, you would hear only the correct two words; otherwise, you could easily get confused and incorrectly believe you also heard the familiar M2 + M2 word (CDE). Testing for this confusion was her Experiment 1.
From this experiment, how did she came up with the idea reported as "infants have absolute pitch"? Because the infants reacted to the fake-out "middle" intervals. The babies seemed to recognize that these intervals were new combinations, despite their being identical (relatively) to other familiar patterns-- while Experiment 3 showed that adults were fooled by the (relative) middle intervals.
But how can you be sure that the babies are really reacting to the fake-out intervals as unfamiliar pitches instead of merely less familiar intervals? Saffran's Experiment 2 attempted to combine the words in two-tone sequences to try to make the babies show that they recognized pairs of absolute pitches as familiar, but it didn't work... at all. The babies didn't react any differently to the supposedly "familiar" or "unfamiliar" sounds. Saffran offered a number of possible reasons for her results, but the most comprehensive analysis seems to have appeared by way of a footnote from Laurel Trainor:
...[I]n Experiment 2 of Saffran and Griepentrog (2001), for example, which tested for relative pitch, three-tone "words" were created... [but] there is no evidence that infants group the familiarization tone streams into triplets of tones rather than pairs of tones. In fact, pairwise statistics would be easier to compute, and therefore, this is probably the major statistical information that infants in fact do encode. This is compounded by the fact that Saffran and Griepentrog defined "pairs" differently for relative and absolute pitch. For absolute pitch, pairs are composed of two tones whereas for relative pitch, "pairs" are composed of three tones... This is very misleading. If infants do in fact encode primarily two-tone rather than three-tone statistics (which is very likely), then the test items in Experiment 2 of Saffran and Griepentrog do not distinguish between the two familiarization conditions... [as] all relative pitches are equally present in both streams. ...Therefore, if infants encode the relative pitch of two-tone pairs (which is what they most likely do), then you would expect no difference in looking times between the two sets of test items, which is exactly what Saffran and Griepentrog found. ...Our conclusion is that infants in these experiments are behaving exactly as one would predict if they encoded the relative pitch of pairs of tones.
Saffran gave it another shot in 2003, repeating her previous experiment exactly but keying the entire experiment to C-major. The infant results in Experiment 1 turned out exactly the opposite (explained now as a "familiarity preference" rather than a "novelty preference"), and experiment 2 was again a total dud (i.e. no difference), while the adults suddenly performed equally well in the absolute-pitch condition. Unfortunately, this doesn't really change much; Experiment 1 could still be explained relatively, Experiment 2 has no result, and Experiment 3 could be explained by the observation that adults, fixed to C-major, could be easily identifying relative scale degrees rather than absolute pitches.
She seems to have given up on absolute pitch since then. Her 2005 study basically acknowledged that when you stick to interval pairs, infants do just fine, which is the essence of Trainor's comment.
However, I do not think Jenny Saffran was on the wrong track. Rather, I suspect she was using a mismatched analogy in replacing syllables with pitches-- meaning that the musical experiment, which was intended to be exactly identical to the linguistic experiment, was in fact totally different.
A syllable is in no way comparable to a single pitch. Each syllable featured in Saffran's linguistic stream is composed of exactly one consonant and one vowel. Every consonant-- a sound defined by its disruptive characteristics-- creates a percussive "downbeat"; speak any portion of her sample stream out loud (bidakupadotigolabubidaku) and you'll find it's quite impossible to avoid the thudding rhythm of the consonant and its long vowel (you can't mix short and long vowels without creating the tell-tale stress patterns and implicit word boundaries Saffran was trying to avoid in the first place). And every vowel is itself, literally, a musical interval. Consequently, far from being a continuous stream of simple sounds, a syllabic sequence is a series of discrete and complex sound-packages, each of which inherently contains-- and conveys-- both rhythmic value and internal musical relationships.
But consider for a moment: Saffran's syllabic experiments are successful. Not only does she show in multiple ways that unconscious statistical analysis, along with exposure to stress cues, is how we develop our perception of language-- as children or adults-- but she takes it a step further to demonstrate that this is how we learn which sound combinations should be given meaning. As an example of this step, children exposed to the (nonsense) words dobu and piga were able to easily use the words as object names, but were not able to create names from the same syllables in unfamiliar configurations (e.g. pido or gabu).
Restated: To recognize words and make them meaningful, our minds extract statistically probable sound combinations from continuous communication streams. Saffran's research suggests no less a conclusion than that this is how we learn to perceive any language; and, furthermore, that we learn to assign meaning to the individual components of language because they have become familiar to us through constant exposure to those same streams. Consider this assertion for a moment: we are readily able to learn components only when they have already become statistically familiar to us. We do not learn components independently for the sake of "building" or even "decoding" a stream; indeed, by attempting to "build" or "decode" a series of sounds (say, through phonics training, memorizing vocabulary lists, or musical interval training) then that series ceases to be a meaningful stream of communication. Rather, we learn components as a way of capturing the identity of certain combinations which have already, naturally, statistically, made themselves known to us.
Let's say, then, that we wanted to re-create Saffran's syllabic experiments with musical stimuli. Each "syllable" would need to contain at least one "consonant", or rhythmic value, and one "vowel", or musical interval. I say "at least" because this would directly imply a series of tone pairs with every other tone played as a duple downbeat, and her 2005 study seems to indicate that downbeats are not necessary with tone pairs; what would be more interesting, I think, is suggested by her work with stress patterns-- that equal success might be achieved with tone triplets in an explicitly 3-beat rhythm. In other words, you could use her strategies to directly induce children to naturally learn trichord structures, and to learn those structures as meaningful, fully-integrated musical components.
To be sure, this new experiment has nothing to do, immediately, with absolute pitch. However, it seems enticing to imagine that the effort could be taken one step further-- that, by their statistical frequencies of their appearances, perhaps even within these same chord-words, absolute pitch information could also be extracted and made meaningful.
I became curious enough about my previous assertion to do something about it: I wrote a program to present the musical tones and asked people to try it out.
The idea is this. Humans naturally try to segment streams of input into chunks. For example, if I type 123123123123123123123, you will quickly recognize this is a regular repetition of "123". Even though it would be equally true to say that it's actually 12's and 3's, or a bunch of 312's with some extra digits on each end, an unbiased and passive examination of this sequence essentially forces the "123" segments into your mind. You can, of course, make yourself see the 231's (or whatever other pattern you like), but "123" is the one you'll see most naturally without deliberate effort.
Whatever the input-- syllables, numbers, shapes, or just about anything presented in sequence-- segmenting a stream of input is an ordinary human process. We seek out the repetitions and put them together. It's just what we do. To quote from Barbara Tillman, "one fundamental characteristic of the cognitive system is to become sensitive to regularities in the environment via mere exposure to its structure."
Saffran tried it using musical tones. In one experiment, she created a randomized repetition of the three-note groups (G#A#F), (CC#D), (BF#G), and (ADE). If you listened to a three-minute stream of these tone groups, even without knowing what you were supposed to be listening for, you'd be very likely afterward to choose this set of tones than this set when asked, "which of these two is more familiar?"
I started by replicating her experiment. I also created a "control group" who didn't hear the three-minute stream, in case there was something inherently familiar about any of the groups (like C-A-F would have been, for example, or C-F#-G). Then I added two more conditions. Because I think that syllables are more comparable to groups of three, and a syllabic sequence has a built-in rhythm, I had people listen to a three-minute sequence that had a prominent 3/4-time downbeat. And then, to find out if this was like picking out syllables, I exactly replicated the first part of Saffran's latest syllabic experiment, replacing each syllable with a group of three tones that had downbeats (and using adults instead of babies).
Going in, I expected that Group 1 would get about 50%, or random chance; Group 2 would do noticeably better because of their exposure to the stream; Group 3 would do better still because of the added downbeat missing from group 2; and if all these turned out as expected, then I could probably be confident that Group 4's results would be a legitimate parallel between tone-groups and syllables.
And here's how it turned out, with four people in each group. 50% is random-chance level; there were a few musicians in Group 1 and Group 2 but no musicians in Groups 3 and 4.
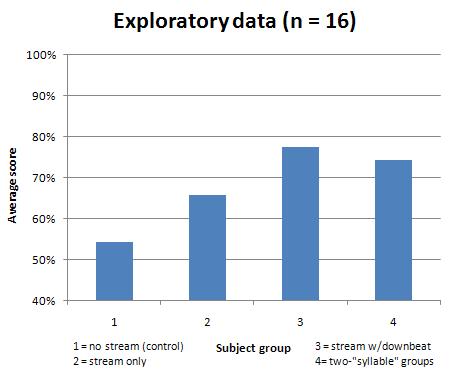
So it looks pretty much exactly like I expected it to. The fact that there are only four people in a group is, at this point, both good and bad; bad because it's not "statistically significant", but good because there doesn't seem to be any ambiguity even with so few people.
The point of this exercise was to see what happened with Group 4. In Group 3, I expected the downbeat to be such a blatant cue that people would do extremely well; after all, if you heard someone say badomipa, you'd be more likely to hear it as ba, do, mi, pa than anything else. But in Group 4, even if people had grouped together the three-tone sets with perfect accuracy, that was no guarantee that they would also group together the pairs of sets. If (CC#D)(ADE) were presented together in the initial stream while (CC#D)(BF#G) was not, then a person who learned only the groups of three would be happy to choose either pair, while a person who had unconsciously learned the pairs would prefer the first pair as "familiar".
And although my result isn't statistically significant right now, it seems likely that more data wouldn't drastically change what seems to be going on. People not only seem to be unconsciously learning the pairs, but they're better at it than they were at learning the three-tone sets-- the sets without the downbeat, that is. This result implies both that there are different levels of grouping that I can manipulate and that even non-musicians do well at it.
What does it all mean? I'll take a shot at explaining where I'm going with this... next time.
Making a comparison between color and pitch is irresistible and is indeed often done. The most consistent objection I've received to making the comparison, though, has been that sound and vision are received differently by the ear or the eye; sound is broken down into all of its component frequencies, but the eye receives three primary colors. Because it is possible, therefore, to (subtractively) combine blue and yellow to make green, but not possible to combine G and C and get E, I abandoned any connection beyond mere analogy.
However, I found myself yesterday in a head-slapping moment when it suddenly occurred to me that our eyes' receptors are red, green, and blue-- or long, medium, and short waves. Where the ear decodes sound into imprecise combinations of frequencies (the basilar membrane is not digital) which are mathematically reassembled in the brain, so too does the eye decode light into imprecise combinations of frequencies which are mathematically reassembled in the brain. In either mode, the input may result in a single perceptual unit. Now, why one of these might be interpreted as a single color while the other might be interpreted as pitch plus timbre is a deep question, but for the moment I'm satisfied to know that they really might be more similar after all.
Here's how Saffran (2003) describes the problem to be solved:
Imagine that you are faced with the following challenge: You must discover the underlying structure of an immense system that contains tens of thousands of pieces, all generated by combining a small set of elements in various ways. These pieces, in turn, can be combined in an infinite number of ways, although only a subset of those combinations is actually correct. However, the subset that is correct is itself infinite. Somehow you must rapidly figure out the structure of this system so that you can use it appropriately early in your childhood.
Her answer seems counterintuitive: by mere exposure to this "immense system" your mind automatically detects the pieces and figures it out for you. Although I'm generally disinclined to give credence to "genetic" explanations of language acquisition, this segmenting process is both extremely powerful and totally hard-coded. It's what our brains are built to do.
Imagine a baby who has yet no idea that "language" exists. This baby nonetheless keeps hearing the sound "bottle" appearing over and over again in his environment. This sound appears often enough that he starts to notice its repetition, and in noticing he wonders what this sound could be. Then, at some point, he hears "bottle" in conjunction with a visual indication of a bottle-- aha! That's it. The sound "bottle" must represent this object here. Now, he thinks, I can say "bottle" to refer to this object.
However-- if I've been understanding correctly, what makes this process counterintuitive is that it happens most effectively when "bottle" is buried inside a load of other words. If you say things like Would you like your bottle? or Here's your bottle for dinner, a baby will learn the word very quickly, but merely repeating "bottle, bottle, bottle" while waving a bottle in his face might produce no learning at all. Words must be inferred from a larger structure. You don't learn the pieces (syllables, words, etc) so you can understand the system; the system itself teaches you the pieces. [Naturally I'm glossing over all the developmental magic of which no one yet has even an inkling. Why this process should happen at all, I don't know, and I probably never will.]
This observation directly contradicts all standardized language instruction, with its vocabulary flashcards and textbook chapters for every verb tense. The more you think about how language is actually learned, though, instead of how it's traditionally taught, the more sense it makes. Young children first start making sentences with the most obvious words, like "want ball" or "give bottle", because they can extract these oft-repeated syllable groups as concretely affixed to their associated concepts. And then, because these words are embedded in a larger stream, the children start to realize that hey, there's something else that word usually goes with, and they begin to say "want a ball" or "give me bottle". And once they know these groupings, they start to notice more consistencies, which provide more words and more grammar, and so on. This seems to be the description offered by Saffran (and other language researchers) of how the initial extractions (segmenting out the syllable-groups which make words) give rise to larger and larger structures until it becomes an entire language.
But this won't help you read or write. Not immediately. Although I would agree that aural communication has to come first, and that reading and writing exist to communicate language after it has already been learned, "reading" is not matching visual symbols to spoken language.
It can't be; the smallest unit of vocal speech is the syllable. Not letters, and not phonemes. Learning vocal speech does not automatically teach letters or phonemes. As the study of the Portuguese illiterates shows, phonemic awareness in spoken language occurs as a consequence of learning to read. Without being explicitly aware that there is such a thing as a "b", the word "bit" is one impenetrably unified sound. Furthermore, co-articulation masks the individual character of any phoneme, so it doesn't solve the problem just to learn to recognize a "buh" sound and call it "b"; Steven Pinker has described how adults can spend a year (or more) successfully learning non-native phonemes but then completely fail to recognize those same sounds in words. It doesn't even seem to be enough to be able to say "buh" and know you're producing a "b", because when you say "bit" you're articulating the syllable bit, not the phonemes buh-ih-tt. This must be the same effect by which a person can learn to sing any song you please, and sing it perfectly well, and yet have not the slightest idea of which intervals they're actually producing.
This is the reason, in fact, why attempting to learn music by memorizing and reproducing "pieces" is counterproductive. In multiple sensory domains, learning a complete object causes active suppression of its individual characteristics-- and the better it's learned, the less aware you become of its components. This holds true whether those characteristics are directly observable features or abstract relational rules. Last week, a woman visited our department to describe the research she had been conducting on the equal-tempered Bohlen-Pierce scale. She wanted to train non-musical people to recognize grammar in the new system, and did so in the same way as Saffran had (and I, in my exploratory study); that is, her subjects listened passively to melodies constructed according to certain rules, after which they were asked to decide which melodies were "good" and which were not. Among everything she had to say, this is what I heard most pointedly: when the subjects were exposed to 10 different melodies (repeated 50-100 times), they learned to recognize those 10 melodies with nearly 100% accuracy... but learned nothing at all about the musical "language" from which those melodies had been constructed. They were completely unable to tell whether an unfamiliar melody did or didn't follow the same rules. By contrast, when her subjects were exposed to 400 different melodies only one time each, they became able to select unfamiliar melodies as "good" or "bad" and to recognize any of the 400 melodies besides. Her subjects were no longer recognizing a limited number of melodies they'd memorized, but had instead learned the grammar by which they could identify an infinite number of melodies.
It is evidently true that from listening we learn grammar, words, and syllables. Letters and phonemes are taught by reading. It would seem obvious, then, that to teach reading one must teach letters and phonemes. I wouldn't disagree with that, especially not after a recent conversation with Betty Ann Levy, who insisted that "cracking the code" was crucial. But phonics training is not the answer because of a basic assumption which, until this same conversation, it hadn't dawned on me that I had inadvertently accepted myself. I had for some time understood that language learning was a "top-down" process, in which larger structures are gradually segmented into increasingly smaller units, and the listening studies essentially confirmed this understanding. I had therefore started to imagine that learning a written language was a double-sided process; the language itself was learned by breaking larger chunks into smaller ones, while literacy was achieved by learning how to put components together to form ever-larger units. But no; that is a backwards approach to literacy. It is critical to learn the components of writing, the letters and phonemes, yes-- but not so they can be used to "build" units of language. They must be learned to complete the decoding process.
Reading by phonics is actually encoding, not decoding. This clip of the Electric Company silhouettes certainly appears to be showing that c and ut can be joined to form cut-- but I'd say that it's really meant to teach that cut may be broken apart to produce c and ut. By themselves, the phonemes c and ut mean nothing, and they will persist in being meaningless until they are co-articulated into a syllabic unit which is physically and perceptually neither one of them. If anyone-- child or adult-- learns to read by putting phonemes together instead of breaking apart words, their "reading" process will be that of constantly encoding streams of meaningless sound, and only after they have finished encoding can they understand what they have "read". But this is how most people are taught to read; besides myself, I have only ever met two people (that I know of) who do not read by encoding.
By no means is this an argument for any kind of "whole language" system. Without explicit knowledge of letters and phonemes, decoding stops at the syllable and fluent encoding is of course impossible. (This amusing anecdotal description neatly describes the failure this inevitably leads to in adult life: "The sheer unpredictability of listening to her read is astounding.")
What I am suggesting is that the most effective and natural method of literacy training will be predicated on the perspective that all written communication is decoding, not encoding. Reading and writing. You may disagree with the way I am using the terms "decode" and "encode", and I agree I am using them unconventionally in the hope of clarifying the processes I am trying to describe. By "encoding" I mean the joining together of meaningless symbols for the purpose of creating meaning. By "decoding" I mean the generation of meaningless symbols from existing meaning-- and in this view, writing must be a process of decoding. It doesn't matter whether you're writing something new or transcribing a speech; mentally or aurally, you are decoding a meaningful linguistic stream into meaningless letters. I don't care if you prefer to call this "encoding" rather than "decoding", as long as you recognize that I am describing a process in which meaning precedes writing.
I strongly suspect, now, that this will serve to explain why I read the way I do. I seem to apprehend text structurally, and while reading I am both totally oblivious to and completely aware of the component sounds. I believe this may be the same kind of process I've already described as applicable to verbal language, of seizing on smaller segments and using them to build ever-larger chunks, but I can get back to that later. The question that's been underneath everything I've written in this article is one I finally faced up to the other day: why does absolute pitch seem to be an inability?
Until recently I've been completely dismissive of the "inability" of absolute pitch. When Miyazaki and so many others pointed at the known detriments of absolute pitch ability, I merely shrugged and answered that not all absolute musicians have these problems, so absolute pitch can't inherently be an inability. But finally I considered, well, what if it is an inability?
The musical studies have shown that, through ordinary listening, anyone may learn the grammars and segments of musical "language" regardless of their supposed musical capacities. But mere listening does not drill down any further than the syllable. I place the linguistic "syllable" at the same structural level as the musical "chord"-- but even if the interval were a syllable the conclusion is the same: spontaneously hearing phonemes is abnormal.
Which leads me to suspect that there are three populations of absolute listeners.
1. If, without any specific training to do so, a person spontaneously begins to interpret music as a series of pitches, some abnormality in their brain may be causing it. Their brain could have a deficit in its ability to perceive linguistic structure. An abnormality that fixates on phonemes at the expense of linguistically meaningful units would prevent their relating to music in a "normal" way and explain many, if not all, of the usual handicaps. Perhaps this is why populations of mentally damaged children (autism, Williams syndrome, at least) show high proportions of absolute pitch. Do these populations also have linguistic difficulties which could be explained by the same phonemic tendencies?
2. If a child is explicitly trained to recognize and remember pitches, but this knowledge is not integrated with other musical instruction, that child may learn music as a process of encoding absolute pitches rather than of decoding meaningful musical structures. This too would lead to the usual inabilities, and I have met a person who described exactly this problem for precisely this reason.
3. And then there is the person for whom absolute pitch seems to be a help, not a hindrance, and any reports of these people generally concur and concede that their musical skills are phenomenal. I have personally met only one such person, but I know of at least one other. Their absolute awareness seems fully integrated with their structural skills, which makes me wonder. Could it be that this type of absolute musician is one who learned their musical skill as any language, and when learning how to decode from song to melody to phrase to progression to chord to interval they-- for whatever reason, in whatever manner-- simply took it one step further, decoding into pitches?
The problem with trying to investigate the validity of this proposal-- these three populations of absolute listener-- is that absolute skill is rare to begin with and trying to find enough people belonging to the third group to mount any kind of statistically useful study is not feasible with my current resources. What I can do for the moment is to assert that these three paths to absolute pitch ability exist, only one of which is indisputably valuable to musicianship, and that the valuable skill occurs as a result of natural segmentation. The studies have already shown that musical segmentation does occur through linguistic listening and training; if the valuable skill is achieved through decoding natural segments into pitch units, then it should be possible to teach absolute pitch by first inducing discovery of the segments through active listening, and then teaching how to decode the segments with reading and writing.
Letters don't exist.
I'd include "phonemes" in that statement except I want my point to be unambiguous. Letters do not exist. We don't think them, we don't hear them, we don't say them. You and I produce our linguistic ideas in "sentences" which, aurally and mentally, manifest themselves as words and syllables-- and when we write, we produce the syllables by decoding them into a combination of alphabetic symbols. If you say at this moment no, wait a minute, of course I write letters, I would suggest you observe yourself as you're writing (or typing), and ask, are you really thinking every single letter to yourself as you write it?
Letters, as sounds, do not exist.
Of course I don't deny that there are people who do think every single letter they write. Take a moment and imagine a person who has to say each letter as he writes it. It's not a flattering image, is it? But nonetheless, even as you imagine this unfortunate, you must acknowledge that he must be thinking of the correct syllables and trying to figure out how to decode them into letters-- and this, I would argue, is because he intends to convey meaning, and letters do not exist as meaningful sounds.
I also can't deny that there are people who think every single letter or phoneme they read; this, sadly, is far more common, trained into some proportion of the populace through phonics training or other "build-a-word" instructional methods. To this point I would reiterate-- the meaning of a written passage is not comprehended until the phonemes are combined into syllables. (I would also suggest that the exhausting, irritating, endless task of combining phonemes is why so many people learn to dislike reading.)
Why, then, are you able to read this: "A B C D E F G"? Because, I would say, what you are speaking and thinking are not letters but words. This is not a minor point, nor is it a clever semantic trick. The units of the alphabet are, every one of them, concepts in their own right. Most of us have been fooled into thinking that a letter is a sound, but Gabe knew better.
Therefore I am describing the process of writing thusly: you conceive an idea, and mentally transform it into a statement; to fulfill this statement you generate words; and to represent words you use letters to write their syllables.
A "letter" is, and is nothing more than, one of the squiggles you use to spell out a syllable. Their combination is arbitrary and, for that matter, merely suggestive; letters do not "make sounds". Words with superfluous letters (subtle, would, knife) immediately spring to mind, but of course there are also the British words Worcestershire and Leicester, so confusing to Americans who encounter the printed words before hearing that the syllables are Worce/ster/shire and Leice/ster. D may be for Dog, but this does not mean that "D makes a duh sound"; this statement teaches that dog is spelled with a D, and that the symbol D is a "dee".
I am hereby asserting that we learn letters-- our concept of "letters"-- not as sounds, but as symbols of syllables' theoretical components. We learn letters because they are used to decode words. We learn letters as units of code, and the sounds associated with these units ("see", "aitch", "eff") are the words we use to describe them.
It may already have occurred to you to think of the common practice of remembering an interval by associating it with some familiar song. Regardless of your opinion of this method, I think you'll have to agree that a person who uses this approach has actually learned an alternate name for the opening of a song, and not its abstract "interval" sound; they can't recognize another interval of the same type without actually comparing it to the known song. Nonetheless, I read in a study recently (but didn't make note of the citation, unfortunately) that it doesn't require the least bit of musical training for anyone to remember and recognize the first interval of a favorite song. Non-musicians do not know the sound of the interval, but know its abstract function for decoding the known song-- and the result suggests, yet again, that we naturally extract smaller units from larger structures when the structures are meaningful.
Despite the fact that intervals and vowel-phonemes are physically identical, and there is no direct parallel to pitch component in a non-tonal language, it seems to me that the process of learning letter-concepts would nonetheless apply to pitches. That is, I would speculate that when pitches are learned, in a musically relevant and non-brain-damaged way, it happens for the purpose of decoding chords. Pitches are related to the objective "scale" in the same way as letters are related to the "alphabet"-- a convenient way to remember the series, organized not by a supposed inherent quality of "low to high" but from the arbitrarily and meaninglessly chosen "first to last". Pitches are meaningfully related to chords, and to the tonality of a musical piece, because they are the units with which either of those structures may be decoded. Pitch sounds may be learned from the process of decoding those structures. Being able to name the individual notes would (as with letters) occur as a secondary effect of decoding the chords (syllables). Knowing an "A" pitch would be a result of knowing how to decode various A-chords, just as knowing "ch" is a result of knowing how to decode various "ch" words.
And this brings us right smack up against the main problem. How would an adult recognize the difference between an A-chord and any other chord with the same relative structure? While I don't yet know what the method for this process will be, I can at least describe the tendency we're working against.
Adults use relative height evaluations to make absolute judgments of pitch. This was the big surprise for me not too long ago. While still in Indiana I did a secondary study to assess note memory through melodic associations; as I expected, the results were all over the place depending on each person's existing musical aptitude, but there was a consistent trend: even those who failed to improve at naming notes did increase their proportion of semitone errors. This confirms for me, at least-- I believe it's too speculative to get published-- that whatever method you use to become able to name notes or recognize chroma, you're still making a relative judgment versus the overall musical spectrum. Adults who learn to name notes are learning to make narrower divisions of the relative range of musical sound. They are not learning absolute pitch. These relative judgments can be quite exact, and need not be hit-or-miss; it's not the accuracy at issue, but the nature of the judgment. As I've taken pains to argue at various times, recognizing pitches based on any overt sensory quality-- including height-- is not making a true absolute-pitch judgment.
There must be some way to differentiate between the pitch sounds not with sensory impression, but with meaning. Absolute pitch may be learned from decoding chords, but you can't decode the chords correctly without absolute pitch ability; this seems to be a Catch-22 on the face of it, but I suspect it may not be with this change in view: maybe absolute pitch is learned from decoding chords because you can't decode the chords correctly without absolute pitch ability. It's pretty easy to imagine that decoding chords would make it possible to learn intervals handily enough, because the internal structure doesn't change regardless of the transposition; what I need to figure out is how to make the tonality of each chord meaningful.
Here's a good example of how reading is a matter of decoding rather than encoding. If you look at the second sketch of this clip (sit or click through the song), you'll see them confused by the word "weight". Building the word phonetically (encoding) results in wee-ee-guh-hut, but the moment they realize "that word must be weight!" they can look at the word and understand its letters (decoding) perfectly well.
I would say that this describes how we learn to write. Segmenting a communication stream teaches words; reading decodes these words into letters, after which the words can be written. That is to say-- the more you read, the better you will write.
Or, more accurately: the more you read, the more it affects your writing. This fact alone explains almost all of the errors collected by Paul Brians. One of the most obvious illustrations is the it's/its confusion. Grammarians writhe and rage about this problem and scream to anyone who will listen, "It's is a contraction of it is! Its follows the form of his, hers, its! If people just took a split second to think about it they wouldn't make this mistake!" But that's the issue-- when writing, we don't think about grammar. The only time we really pay attention to grammar is when we're revising (or deliberately trying to be clever) and paying attention to construction instead of communication. When we communicate we spell words instinctively, in the ways we've seen them written. I personally don't enjoy seeing "it's" as a possessive; every time I see it I feel like I've been poked in the eye. The fact is, though, I almost never see "its" written correctly. Popular grammatical errors are self-perpetuating, especially now when most writing we're exposed to is unedited, unmoderated, and informal. When people see the possessive pronoun written as "it's" 19 out of every 20 times, how could they possibly not learn "it's" is correct? Even when they're explicitly told otherwise, 95% of everything they read will contradict what they've been told, and they will remember and write what they've learned about writing, not what they've been told about grammar. (For this reason, I assert and maintain that trying to "correct" someone's writing is a complete waste of time. If you want someone to learn better grammar or spelling, you must give them better reading material. There is no other way to do it.)
To write, then, we decode ideas into letter-structures which have been familiarized through reading. Imagine yourself transcribing a sentence and you'll realize that you're doing exactly this, remembering the meaning and decoding it into words you've read. When you hear a word you've never read before, regardless of whether you know the word, you have to ask how do you spell that, or take your best guess based on words you have seen. By comparison-- have you ever tried to transcribe a sentence in an unfamiliar language? It's practically impossible to do by listening; you don't know how to segment out any of the words, much less how to spell them. But it's also very difficult to retype a foreign sentence, despite having the text right there in front of you, even when it uses alphabetic characters you already know. You can only type it by encoding, character by character-- and sometimes sound by sound; although you can't be sure that it's the correct sound in your head, it still comes out of the keyboard correctly. With enough practice you may be able to recognize commonly-used words and type those from memory, but these familiarized words are merely oases of still-meaningless groups of sound in a larger morass, and once you've exhausted the tiny spurt of speed afforded you by that word, you're forced to return to letter-by-letter encoding. In short: you only reproduce language sound-by-sound when you don't know what it means.
I hope you've drawn an immediate connection to music as it is normally practiced. As far as I know, most people's idea of "playing" a piece of music is to encode the notes, one by one, off the page-- and to transcribe "by ear", I have seen nationally revered and reputable musicians advise and instruct that a composition must be unraveled interval by interval, sound by sound. Therefore in either case, reading or writing, nothing meaningful is being communicated. If the premise is accepted, the conclusion is inescapable:
If music is a language, most musicians do not understand it.
I'll show you what I mean. Here is a sentence: "I have ants in my pants." Now if I ask you to paraphrase that sentence, without using any of the words I just wrote, can you do it? I would be very surprised if you couldn't. If you're finding it difficult that could only be because I may have asked the question poorly; otherwise, with a little thought, you'd easily come up with "there are small insects crawling up these trousers" or its equivalent. Because you understand the language, you can recognize and extract the essential idea of any sentence.
Now, here is a musical phrase. Can you paraphrase it?
I know I couldn't. I don't recognize the essential idea in the first place-- I don't know what the language is telling me-- so I couldn't possibly extract it. I can't communicate the meaning of this phrase without using exactly these "words" provided by the composer. How many musicians do you know who would be able to "say" a musical phrase without reproducing exactly what has been notated? Is there an amateur musician on the planet who would have the slightest idea how?
I had wondered, weeks ago, how a musician would rewrite a composition. How do they know what is weak, what could be added or deleted, or what needed to be changed? The answer, I've realized, is the same as how I revise anything I've written. I have an idea to communicate; therefore I replace and rearrange words until my idea is communicated most clearly and effectively. This happens in music, too, and I'm not just talking about theme and variations. A composer can write a respectable but unremarkable song, and then someone else comes along and says wait, I think I get it, but isn't this what you meant? and a pleasant little ditty becomes a number one jam.
I might say the genius of a musical composer is in the clarity of his expression. I remember David Letterman once claiming "The Mission Impossible theme makes anything seem exciting!" and playing the music over a fixed camera shot of a dumpy, half-dressed, middle-aged man wandering aimlessly around an unkempt apartment, scratching himself and eating cold cereal. Whether or not the music makes you feel excited, it successfully communicates the idea "something exciting is happening." You can experience the same effect about one minute into this clip; imagine watching the scene with only the dialogue and no music and you'll see what I mean.
The pursuit of this observation leads to the question: what does music mean? What is a "musical idea"? What do you "say" with music?
I do have an answer. Although I couldn't begin to conceive the cosmic mystery of what does music mean to humanity? I have a firm opinion of what music, as a language, will communicate: emotion. I've said as much as this before, and I believe I've also clarified my statement to assert that music communicates emotion directly, unambiguously, and objectively. It is a critical mistake to believe that musical communication occurs solely when a listener is made to sympathetically feel an emotion, just as it would be incorrect to believe that you can understand my words only when you agree with me. You can comprehend what I write without adopting my ideas as your own; you may disagree altogether, but you will understand what I'm saying.
How can you make a non-musician comprehend a musical idea? The best approach I've figured so far is this-- imagine yourself speaking with the musical tones and ask yourself, what feeling would I have to be expressing to use them? The best example I've found of an unambiguous musical idea is this one: watch out. Speak these tones out loud under the words "watch out", as close to the original timbre as your voice will allow, and notice how you would have to feel to say them this way. The tones' relative stability and easy tempo suggest that the danger is not yet imminent, that there is still a chance of safety and escape, while the deep timbre indicates this concern is serious and grave. As the tune develops, imagine yourself gradually realizing that the person you're trying to warn isn't listening. The drumbeats punctuate hey! HEY! as you try to get their attention; the tempo increases as you increase your efforts, and as you become worried and frantic the music introduces new notes of tension and dissonance in harsher, crying timbres. So, now that you have the idea-- do you think you could say this same idea using different musical sounds?
I would argue that everyone already is musically expert, regardless of formal training. We receive informal training all our lives, and not just by "listening to music". Every sentence we hear spoken contains musical ideas, whether we know it or not, which we receive and interpret with great precision. Every sentence we speak generates a musical idea which is an unconscious expression of our emotional intentions and overall body state. The wonder of music is how, like language, it is capable of infinite complexity and subtlety, but musical composition at its most basic level expresses, biologically, "this is how I feel right now." Listen to anyone speaking and you will hear exactly this happening; any boring ordinary conversation reveals surprisingly sophisticated musical activity if you ignore the words and listen to the tones and rhythms. I suspect an important step is recognizing that music-- the purposeful expression of music-- is not best described as a series of "chords" or "intervals" or any other abstract musical terms, but as a sequence of tensions and relaxations relative to a tonic. Relations between tones may be meaningful, but interval relationships are a subset of the same tones' relationship to an overall message. Measured by "distance" alone, a minor second is never anything other than a minor second, but in a tonal context di to do says something completely different than sol to se.
Tonality seems to be emerging as the natural focal point. The other day I was contemplating how someone without absolute pitch could possibly learn to tell apart different chords objectively, and not with any kind of relative measures. What objectively distinguishes an F-major from a G-major triad? I considered how in Chordhopper I learned to avoid confusing F and G by associating their chords with familiar music. The orange ticket (FAC) and the blue fish (GBD) have the same major-triad structure, but the ticket is the first chord of Ob-La-Di and the fish isn't. The orange basketball (ACF) is the first chord of My Country 'Tis of Thee, and the blue marble (BDG) isn't. Now that I have these associations, although I still perceive these chords are "near in height" to each other, "height" does not guide my judgment. Instead I can decide, objectively, whether or not a chord begins a familiar song. This is not the end of the story, however. For one, I stopped confusing the blue raindrop (DGB) versus the orange flower (CFA) not because of a song association but because, once I had six other blue chords in play, the raindrop seemed to belong with the other blues while the flower didn't-- regardless of whether or not I'd just heard another blue chord. For another, last week I played enough to add all three A-minor inversions (the grey tiles), and now I can distinguish between any blue and orange for another reason: after any grey tile, an orange sounds good and a blue one doesn't. That judgment also has nothing to do with height, and nothing to do with any familiar songs, and everything to do with tonality.
Chords can be recognized objectively by perceiving their function within an absolute tonality. It occurred to me that the chords I had associated with familiar songs didn't start each song so much as they fit with each song. Following a grey tile, the basketball sounds nothing like My Country 'Tis of Thee, but I still know exactly which chord it is because I know I'm in A-minor. And, because I know exactly which chord it is, I can decode it into its component pitches.
The implication is clear: absolute "pitch" ability may in fact be absolute tonality. As I continue forward in trying to learn it and teach it, I'll keep in mind what I've learned from Chordhopper, with the raindrop that "belongs" to blue and the songs that associate with orange, especially remembering the study of the Bohlen-Pierce scale which pointed out that in using only a handful of melodies, people learned nothing but the melodies, but in using 400 melodies, people learned the language.
The authors of the 1979 report of Portuguese illiterates didn't disappear. I've just been reading a 2003 review by the lead author of that original study, and in it he makes a distinction between conscious and unconscious representations of phonemes. He would argue, it seems, that an illiterate person does know the difference between bed and fed because they are recognizing the difference between the b and f sounds; they're not recognizing each word wholly. However, the illiterate listener does not have an active mental representation of the individual sounds. They can tell them apart, but do so only by the raw sound and not by consciously recognizing the phonemes. This makes sense if you remember that a baby learns in its first year to tell one phoneme from another.
I can think of a parallel example in music. If the learning effects of Chordhopper are any indication, then when a person (otherwise untrained in music) is taught to recognize the difference between two very similar chords, they will become fully aware that only one part of the chord is different-- but they may not be able to tell you which part that is, nor even what proportion of the total chord has changed. This person recognizes Chord One and Chord Two as chords, and perceives the similarity between the chords, but they don't know and can't explain what actually makes each one different.
Does this author's concept of "unconscious phonemes" represent the same problem I've been describing in absolute pitch perception? Is a "conscious phoneme", separate as it is from a vocal sound, the same kind of concept as the abstract, height-less pitch reported by the absolute listener? Would an illiterate, if asked to describe the difference, attempt to describe the raw sound of each? A question which I believe has been answered, somewhere, is whether they'd recognize the first sounds of words to be the same as each other-- "Does sand begin the same way as smart?"-- and though I don't know right now what the answer is, I wouldn't be surprised if their perception of phonemes is as contextually variable as any non-absolute listener's perception of pitch.
In any case, now that I've spent the year indulging in speculation, it seems time to get back to the published research. In addition to exploring lexical segmentation and acquisition, I'm going to look at the basic facts of audition (at Laurel Trainor's recommendation). Although I had thought I'd done a fairly good job of teaching myself the basic physiology and neurology, it seems I have overlooked more than I've assimilated. I'm sure I'll end up repeating a load of what I've already written-- but I seem to do that quite a lot anyhow, especially now that I've been at this for a few years. Old ideas will pop up again in new contexts; it's irritating to have forgotten what I wrote but reassuring to know that the old thoughts are still there to inform new directions.