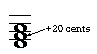
Acoustic Learning,
Inc.
Absolute Pitch research, ear training and more
I was brought into the Percepts and Concepts group principally because of an experiment which Rob Goldstone wants to see conducted: a discrimination task involving chords that have been microtonally adjusted. For example, a subject hears a chord like this one
and then is asked to identify which of these two chords matches it.
Rob's primary interest is, and has been, categorical perception. I've discovered that every one of his publications directly informs my own research in some way, because his basic thesis (and the raison d'etre of this research group) is that mental concepts determine perception. In other words, what we perceive is dependent on our prior expectations, and it's so strongly dependent that until we've learned what to expect, we may perceive nothing at all. This issue is the heart of the perfect-pitch training problem. An obvious visual example of the phenomenon is Droodles. The humor of Droodles is that they are (at their best) completely indecipherable until you know what you're seeing-- but once you do know it's perfectly obvious and true.
The experimental process should be essentially this. I must develop an experimental hypothesis which will predict how different subjects will categorize and decipher these chords; I need to figure out which chords will best test and illustrate those predictions; and by the time I've gotten that far, I hope I'll have answered the question why bother to do this experiment? Somehow, this test and its experimental results should reveal something new about categorical musical perception.
Rob's original hypotheses have by now been done. He thought the experiment might reveal that absolute listeners exhibit categorical perception, but that's covered by Harris 1974, Rakowski 1993, and others. He also wondered, if an interval's microtonal adjustments crossed pitch category boundaries, would an absolute listener judge according to pitch or interval? The answer is interval (Benguerel et al 1991, McGeough 1987, and others). And the broader hypothesis-- that musicians will perceive musical sounds categorically while non-musicians will not-- has also been demonstrated at least once (Siegel and Siegel, 1977). Nonetheless, this experiment does have something that none of those others do: chords. And that opens up a whole new ball of worms.
The first step is to examine more closely what has been done before with regard to categorical perception and discrimination. I've looked at most of these before (in Phase 11) but not for the purposes of this experiment, and I'll only want to carefully revisit the ones which seem to be pivotal. As I look at these, there's one fact I'll want to keep in mind, too, even though I do not yet have a citation for where it can be found: in structural (or "relative") listening tasks, the brain activity of absolute musicians showed no significant differences from non-absolute listeners. So I may speculate, when checking out these papers, that any demonstrated absence of absolute sense is due to an absolute subject's use of structural thinking.
An unfortunate aspect of all of this research is that the subject groups are always divided into three: absolute musicians, non-absolute musicians, and non-musicians. There's never a category for absolute non-musicians. These people exist, and their performance on the experimental tasks would be quite revealing; but even if one acknowledges that there is such a group of people, where do you find them? It's easy enough to go to the musical population and ask "okay, who's got it?" because you have a 1 in 10 chance; but if the ratio among the general population is 1 in 10,000 including the musicians, the percentage of folks who have absolute pitch ability but are non-musicians must be impractically difficult to locate.
This article shows that absolute listeners judge intervals by the interval sound, not the component pitches.
The researchers mistuned tones so that they would form different intervals depending on how they were evaluated. For example, B+40 cents and an E -40 cents form a slightly augmented major third, but B and E are categorically a perfect fourth. The researchers suspected that their absolute subjects might judge intervals by recognizing the pitch components, and thus mis-identify the interval, but this happened only rarely. The researchers thus concluded that absolute listeners were using an "RP strategy" to identify the tones, using the interval categories for identification rather than the pitch categories.
However, the researchers were guided and restricted by their assumption that notes have "distance" between them. This assumption created their predicted "AP strategy"; that is, if you believe the only normal "RP strategy" is to listen to the individual tones and mentally evaluate the "distance" between them, then it's logical to assume that a normal "AP strategy" would be to recognize the individual tones and mentally calculate the "distance" between them... and, given the experimental results, the researchers had to conclude that "most musicians with or without AP use their relative pitch ability to identify musical intervals."
But their conclusion does not explain why one of the absolute subjects sometimes used the "AP strategy". This single subject correctly evaluated the intervals for certain pitches, but not with other pitches; and then, when re-tested a month later, this same subject's responses to the same pitches were completely reversed. It is perhaps not a coincidence that this subject pre-tested most strongly for absolute ability-- and yet the researchers dismissed his result as "inconsistent and thus unrepeatable" without any further analysis.
What makes the result all the more puzzling is that the researchers used only the intervals of m3, M3, and P4. Two of these three are within the critical bandwidth, and might perhaps be evaluated harmonically by all subjects, despite the fact that the trial tones were all sequential (not simultaneous). With these easily identified intervals, why would a subject resort to an absolute strategy at all? The most likely reason, I'd think, would be since the oddball subject was the one who had the "strongest" absolute ability, he could have proceeded through his musical training without making much effort to develop his relative skills, so that even with such easily-identified intervals, the slightest confusion could cause him to fall back on absolute identities.
In any case, regardless of what the strategies actually are, this article offers a strong argument that absolute listening is a fallback strategy for identifying musical structures. The primary strategy is to evaluate the relative structure, and the absolute sounds are secondary.
But does this mean that the fallback strategy is absolute sounds or component sounds? If component sounds are the fallback, then perhaps similar results could be achieved by adjusting the intervals of chords so that the intervals would yield one chord judgment while the overall sound would yield another? For example, if you had a simple CEG chord and expanded the top and bottom tones by 30 cents, then categorically the intervals would still be major and minor thirds, but the C- to G+ interval would be a minor sixth, and the overall chord would sound like this. Then if you adjusted the entire chord down by 30 cents, the C- would drop into the B+ category while the E- and G- remained within their same categories, and that would sound like this. Do both of these sound like major triads to you? Or something else? And would your judgment have been different if I hadn't preconditioned you to expect a major triad? What if the tones of this last chord were arpeggiated? Or arpeggiated and played in descending order? The question of which are the salient features-- not only how we recognize them, but how we prioritize them-- is one I expect my experiment to address.
I've spent the entire time between the last article and this one wrestling with this publication:
Burns, E. and Campbell, S. (1994). Frequency and frequency-ratio resolution by possessors of absolute and relative pitch: examples of categorical perception? Journal of the Acoustical Society of America, 95(5), 2704-19.
This paper is a convolution of logical contradictions and incomplete thoughts. Between its impenetrable writing and its incomprehensible charts I've only been able to chip away at it, day by day, dislodging mere crumbs of information-- I wasn't able to understand their explanations until I understood their experiments, but I wasn't able to understand their experiments without the explanations. Still, I've kept at it, and today I've found the payoff. This paper provides an excellent model for the procedure and analytical context I can use in my own experiment; but it also provides a vivid reminder of normal assumptions about musical perception.
What has made this paper so impossible to understand (aside from its style) is that the writers cling steadfastly to their assumptions even when those assumptions directly contradict known phenomena-- or even their own experimental data. Rather than attempt to discuss or explain the contradictions, they make rhetorical statements ("Isn't this puzzling?") and explore no further. So I kept picking away, trying to get down to the basic facts, down past the overcomplicated sentences and graphs, and yesterday I finally noticed this statement buried deep within the text:
The categories used by AP possessors to classify tones, the note names of the chromatic scale (C, C#, etc) are the exact homologs of the chromatic interval categories used by RP possessors to identify intervals, and they are, of course, both related to the same general process, the perception of musical pitch.
Suddenly all the contradictions made sense. These authors believe that interval and pitch judgments follow the "same general process"-- but interval recognition is a synthesis of musical pitch perception. That's where their problem began, and I soon saw how every contradiction in the paper was engendered by this erroneous premise. For example, I hadn't understood why the experimenters asked the absolute musicians to identify only pitches, and the relative musicians only intervals. I figured the relative musicians couldn't be expected to reliably identify pitches, but why hadn't the absolute musicians identified intervals?
The researchers thought this was the same task! In the researchers' view, there is no difference between intervals and pitches. The researchers think of the spectrum of auditory sound as a "unidimensional psychophysical continua"-- that is, a straight line-- and one pitch as a point on that line. Any two pitches are the endpoints of a segment on the same line, and intervals are identified by mentally measuring segments (or "estimating the extent between two basic sensations", as they put it). So when the interval-judgment data came out as the opposite of the absolute-judgment data, all the researchers could do was declare the result "puzzling" and drop the subject. It apparently never occurred to them that if pitches were perceived in combination, more sensory information would be transmitted, making categorical identification more precise.
Normally, discrimination is better than identification. You can hear this for yourself. Speak the vowel "oo" (as in pool) and then, while still making sound, slowly open your mouth to its widest aperture. It is essential that you do not think of making different vowel sounds; rather, just think of gradually opening your mouth, and listen to the sounds that appear. If you do this, then depending on how quickly you open your mouth you will hear 1-4 more vowels-- and only 1-4 more vowels. Although you can hear the vowel sound changing, it stubbornly remains the same vowel until suddenly and instantly it's a completely different vowel. These are the identification categories (2-5 units). Now say the "oo" again, then open your lips only slightly and speak whatever vowel comes out. It's still the same vowel, but you can hear that it is nonetheless a different sound. This is your ability to discriminate between vowels. As you can hear, sensory discrimination is more precise than categorical identification.
This is what the researchers expected to happen with intervals, but it didn't. Although absolute discrimination ("which pitch is higher?") was more precise than identification, interval discrimination ("which interval is wider?") was much poorer than identification. The researchers readily dismissed the result as inexplicable: "There is no situation... [which] would predict [this result]," they complained.
But it would be predictable if category identification and "width" discrimination were entirely different types of judgment. Intervals might be identified by harmonic synthesis but discriminated using absolute spectral positions. Perhaps, then, "width" is the wrong thing to be discriminating if it's to be compared to identification; after all, intervals are defined as frequency ratios, not widths. By semitone width, the next step "up" from a perfect fourth would seem to be a tritone, but as a ratio this is a drastic change from "4/3" to "45/32". Wouldn't a more appropriate categorical boundary be the next more complex interval-- that going "up" from a p4 would actually be toward an M6 (5/3), while the next step "down" would be toward the p5 (3/2)? If intervals were gradually altered by dissonance, not width, that might produce the expected result.
The researchers were probably thrown by the fact that interval identification and discrimination both seem to resemble normal categorical perception. In categorical perception, identification is easiest around a "perceptual anchor" where the categorical identity is strongest, and resolution is finest at the borders where categorical identity is weakest. Here's a graph which shows that interval discrimination was better at the mistuned borders (50, 150, 250, and 350) than at the in-tune semitones (100, 200, 300)-- that is, notice that the '50s are where the discrimination is greatest.
And here's a graph which shows that identification was better at the categorical centers.
In this graph, I don't think the vertical axis is "proportion correctly identified", because that would make a simple bar graph-- and in their introduction, the researchers said that they selected subjects who were already able to identify musical intervals with perfect accuracy. Rather, I think this graph intends to show how often the subjects categorized each particular interval tuning. The reason the peaks don't always reach "1.0" (100%) is that the subject was allowed to choose quarter-tone categories ("flat major third", etc) and those are represented by the dashed lines. If I'm interpreting this graph as it's intended, then it seems to show how the RP3 subject was much better at identifying intervals at the mathematical center-- the "perceptual anchor"-- of each interval category, whether in or out of tune.
Seeing these results as plainly categorical, the researchers simply didn't suspect that these might be two entirely different types of category. Admittedly, I don't know whether or not this is true-- perhaps that's an experiment I'll have to conduct myself. Regardless of the researchers' overall understanding of the results, and regardless of the type of category which might be applicable, the data does show evidence that interval perception is categorical.
The researchers' misunderstanding of musical category extends into their absolute experiment as well. Because they think of the entire auditory spectrum as a single line, they believe that pitch categories are formed by chopping up the entire line into equal segments; in the paper's introduction, the authors declared absolute pitch ability to be a violation of the 7±2 rule because "the best possessors can identify on the order of 75 frequencies without error." But these 75+ frequencies are nothing more than the same seven pitch categories repeated using additional modifiers (octave, pitch class, and accidental). 7 pitches + 5 accidentals = 12 pitch labels, and 12 labels x 6 octaves = 72 apparent "categories". The absolute judgment of pitch across octaves is a rapid series of decisions, but these researchers drew (or failed to draw) their conclusions thinking that total absolute identity is based on a single unitary spectral value.
Leaving aside all conclusions, though, the absolute data does present an inherent quandry-- it does not show evidence that pitch perception is categorical. For one, the discrimination charts don't show any significant effect at the mathematical categorical boundaries (notice the absence of sensitivity peaks at the '50s)
and none of the identification charts looked anything alike.
The authors scratched their head at this, saying "the most puzzling result for the AP experiment was the lack of obvious regions of increased identification sensitivity which could be interpreted as perceptual anchors."
I'm also not entirely sure why this should be. I wonder if it's a result of the researchers using "pure tones" (sine waves) instead of musical tones. The researchers say they used pure tones simply to avoid whatever clues might be given by audible overtones, and that'd seem reasonable because absolute judgment is pegged to the fundamental spectral frequency of a tone... but on the other hand, it's generally true that absolute listeners often find judging pure tones more difficult (the authors acknowledge this while justifying their choice of pure tones), and perception of pitch is not a direct sensory zap but a mathematical calculation. Could it be that using pure tones stripped away whatever sensory information is normally used in categorical tone perception? Or is it possible that tone perception is simply not categorical?
I don't yet know enough about categorical perception to render a solid opinion, but it seems most probable to me that the researchers somehow ran this experiment in a way which thwarted it. Pure tones may have removed information necessary for categorization; it's also possible that, because the experiments used discrete equally-spaced tones rather than sliding tones (which are, theoretically, infinitely variable within their range), neither the identification nor the discrimination tasks were specific enough or difficult enough to reveal the true absolute strategy. As Boring (1940) points out, and as you heard yourself when you listened to your own vowel categories, "it is easier to perceive a difference when the impressions are separated by a 'contour' than when the one fades slowly... into the other."
It's been a tremendous task this week just understanding this paper. Deciphering enough to have written as much as I have here has been exhausting, and I haven't even started in on its treatment of trace-context theory which I should be able to use to guide my own experiments. The paper's value will largely be in its contradictions; the very problems which caused the researchers such confusion should provide useful procedural tips for me-- such as being aware that mismatched results probably mean mismatched tasks. More importantly, though, is the fact that this paper made it through peer review without anyone objecting to their assertion that intervals were evaluated as a spectral segment rather than a frequency ratio. Most of the people I speak with about musical perception are either completely unfamiliar with the topic, or have their own perceptions to analyze, or have been following along with my lines of thought, so it's not difficult to find common ground for discussion. I don't often try to discuss my theories and understandings of musical perception with people who are thoroughly well-informed in cognitive science but who nonetheless are surprised that intervals don't mean "distance". I will be surprised if what I write doesn't initially cause a great deal of confusion and prompt many people to insist I write more and more clarifications.
On the plus side, it's obvious from reading this paper that I don't need to make a thorough revisitation of everything that's gone before launching my own experiment. I have a pretty good idea of what I want to do, now, and why; I'll design the experiment, run it, and see if what I know can explain the results. If not, then I can dig up more research either to provide the explanation or give me an idea about how to revise the experimental procedure and try again.
Since the Eguchi method is entirely quantitative, I thought the system would lend itself well to scientific experiment and data analysis. I had some initial discussions about the method with some of the researchers here, and from those discussions determined that the best angle on the experiment would be to attempt to eliminate the "Phase 2" stagnation period. I was encouraged because, it seemed to me, the stagnation period could be eliminated by actively and explicitly encouraging children to classify chords instead of forcing them to figure it out on their own.
So yesterday afternoon I stood before the developmental science group to explain the Eguchi method. Right off the bat I told them that I had never actually run an experiment before, so I was making this presentation to solicit their help in evaluating the experiment. Then, having explained the method and my proposed revision of it, as my final statement I acknowledged what I saw as the biggest obstacle to implementation-- that children basically hate it. At this, the head of the group visibly relaxed, although her face became no less sour than it had been for the previous half-hour, and she quickly interjected
I'm glad you recognize that. You can't do this experiment. Putting children through the process you've just described would be unethical.
I didn't offer much objection. I have decried the Eguchi training philosophy, but only on principle; it was something else again to hear a research scientist-- a professional academic who has been experimenting with toddlers and infants for more than thirty years-- tell me flat-out that subjecting children to the Eguchi method would be unethical.
This, of course, would help explain why the method has been completely ignored since 1982. Even if researchers had been made aware of the method by Sakakibara's 1999 and 2004 papers, they wouldn't want to try it. As the discussion developed (following my presentation) it became obvious that if I wanted any hope of pursuing an experiment, I would have to make so many compromises and concessions as to alter the method into something unrecognizable-- indeed, to my great surprise, people began suggesting constraints and modifications which I had already identified in Cohen & Baird (1990) as causing their failure. I had indeed wondered why Cohen & Baird could have so thoroughly misunderstood Eguchi's method when they were in personal contact with her through their entire process; now I see that they may have understood the method perfectly well but simply refused to implement it as Eguchi instructs. Sakakibara had no ethical issues, as she recruited children who were already enrolled at the Eguchi school, and whose parents were thus already willing to endure the process. But me, I wouldn't want any child of mine to be subjected to this system, so why should I try to convince other parents that their children should?
So, quantitative and unambiguous as the Eguchi system might be, an Eguchi experiment is not going to happen-- and for the very reasons that made me reject the "teaching" method.
My biggest surprise came in designing this experiment. I wanted to figure out: if a trichord can be described as either one tonal mass, two intervals, or three pitch classes, which of these do people actually use to identify a chord? So I brainstormed as many different microtonal adjustments of a chord as I could think of which would separate the different sounds.
I described this a while ago, but here is an extended explanation of just that one example. Because a semitone is 100 "cents", you can stretch or shrink any interval by as much as 49 cents and still retain its identity. If you take a normal major triad (major third + minor third = perfect fifth)
and you stretch each of the intervals by 30 cents, you still have the definition of a major chord (M3 + m3), but the interval they form is now categorically a minor sixth:
so if you heard this new chord, what kind of chord would you think it was? A major chord, because of its intervals, or an augmented chord, because of the overall sound? Or perhaps it still sounds like a major chord because the pitch classes are still the same (C-30, E, G+30). If the entire chord is shifted down by 30 more cents, then the top two tones are still in the same pitch classes (E-30, G) but the bottom tone is now a B+40, and the chord sounds like this. Or shift it up instead, so that you have C, E+30, A-40, and it'll sound like this. Still a major chord? Or something else?
I designed more than a dozen of these kinds of manipulations (correct intervals but incorrect pitches, correct pitches but incorrect intervals, correct "outer" intervals but incorrect "inner" intervals) to most thoroughly separate the chords, intervals, and pitches.
Now here's the surprise. When I brought these to Rob, however, he pointed out that I couldn't possibly incorporate all of these different manipulations into a single experiment. To be statistically significant, each of these manipulations would have to be run through dozens of trials, which would mean a single subject running through all of the manipulations I had invented would have to listen to upwards of fifty thousand chords. I had to settle for only two adjustments.
So here's the basic experiment. The first manipulation is to take a trichord and adjust its middle tone to be one of 13 microtonal spaces between minor and suspended; this requires 338 trials (26 trials x 13 conditions).
Then the second manipulation is to do this all over again, shifted by 25 cents, so that the boundaries of the pitches and intervals don't match.
The subjects are either "absolute" musicians, "relative" musicians, or non-musicians.
To make a choice, the subjects listen to a stimulus (X) and then decide which of two other chords (A and B) matches it. This type of presentation was Rob's idea. I had thought it would be enough to listen to only two chords and decide if they matched, but Rob assured me that people are often biased toward choosing "same" or "different" regardless of what they actually hear. Because chord X is followed by Chord A, the subjects can't help but make a same/different judgment, and this may indeed be the basis of their decision; but since there is a chord B still to be heard they will be more likely to keep an open mind.
Back to the original question, then-- how are these chords going to be interpreted? One chord, two intervals, or three pitches? I predicted that the non-musicians would probably judge by the overall sound; the relative musicians would probably identify the intervals; and although the absolute musicians would probably also judge by the intervals, they might become confused when the pitches and intervals were mismatched.
We expected that we'd be able to tell the subjects' interpretation by checking for categorical perception. Absolute musicians show categorical perception for pitches (Rakowski 1993 and others) and non-absolute musicians show categorical perception for musical intervals (Burns & Campbell 1994 and others). Rob Goldstone defines categorical perception as when "differences among items that fall into different categories are exaggerated, and differences among items that fall into the same category are minimized." Therefore items in the same category become perceptually identical, and items in different categories seem totally different even when they're just slightly changed.
This leads to two primary effects which are the hallmarks of categorical perception: people can identify an object more easily when that object is closest to its ideal form, and people can discriminate between objects more easily when the objects are closest to a categorical boundary. An idealized sample of categorical perception would, therefore, produce the following results:
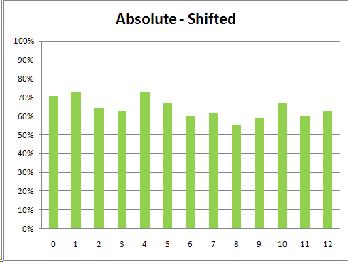
Because this experiment is an exercise in discrimination between two different sounds, it seemed most likely that the subjects' results would most closely resemble the discrimination graph. I was surprised, then, when the musicians' results looked like identification instead, with peaks closer to the category anchors (0, 6, 12) instead of at the boundaries (3 and 9).
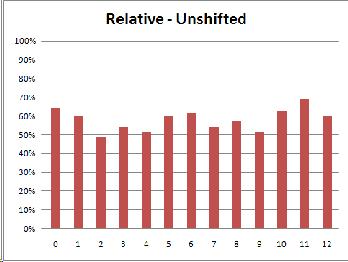
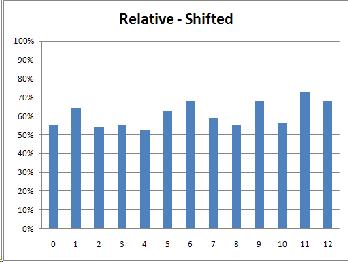
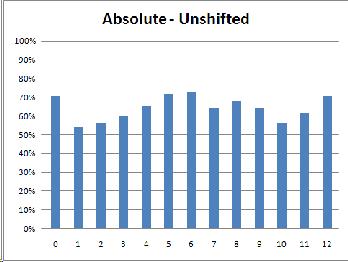
(As was expected, the relative musicians did the same in both conditions while the absolute musicians were thrown off by the shifted condition.)
It certainly seemed that the subjects were identifying chords, not discriminating between them. The most likely explanation seemed to be that the subjects weren't listening to the exact sound of chord X. Instead, they were probably hearing X and identifying it as "that's a major/minor/suspended chord" before matching that identification to A or B. The subjects' self-reports contained hints that this might be the case; one said that he "transcribed the chords in [his] head" as he heard them, and another said "The ones that were easier to spot were the ones that included chords that were actually in tune; if I couldn't remember [chord X] exactly, I'd choose whichever of the two chords was most in-tune."
If this is true, how can I find it in the data? Fortunately, in each trial I kept track of whether the matching chord was higher or lower than the "foil" chord. I charted these separately and took another look. Here's the chart which makes it the most obvious:
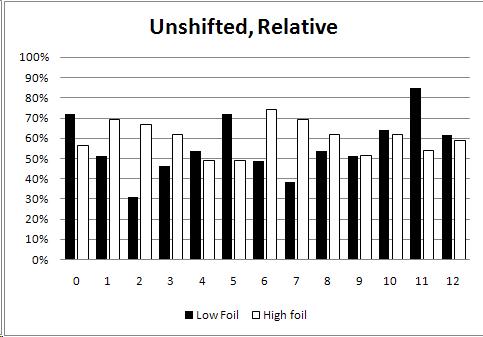
From this graph you can see how, in most cases, the subjects chose between A and B based on which was more in tune. #7 shows this quite clearly; the subjects all preferred to pick the choice nearest to #6 (the in-tune major chord), so when the foil was lower they'd get it wrong, and when the correct answer was lower they'd get it right. You can see this same effect as a trend; look at #2 through #5 and see how the white and black are mirror images of each other as they approach #6.
I will be getting more subjects next calendar year, whose results, I hope, will continue to develop in these directions. With only seven musical subjects total (the above graph represents only three people) these results aren't yet entirely clear or entirely consistent-- but between the "identification shape" of the first graphs, the apparent magnet effect toward in-tune chords, and the subjects' self-reports, it does seem likely.
The bottom line, though: what does this matter? Initially Rob thought that this experiment might reveal a difference in categorical perception between relative and absolute musicians. He thought that the results might show absolute listeners judging by pitch and relative listeners judging by interval-- but that didn't happen. We seem to be finding something entirely different: that trained musicians are not actually remembering the sounds they hear. Instead, they immediately re-code the sounds as symbolic labels ("I'm transcribing in my head") and remember those. Such an effect would explain the subjects' preference for in-tune sounds, and could also explain the absolute listeners' confusion when presented with out-of-pitch chords.
Perhaps, also, it would help explain why traditional approaches to absolute pitch training have always failed-- as training methods have tended to focus entirely on some method of remembering tones (melodies, colors, "feelings", tone qualities) rather than finding ways to symbolically encode them.
Last week I again found myself in the frustrating position of trying to answer: what's the point of absolute pitch? Musicians seem to get along without it, and there's evidence of absolute pitch being a hindrance, so what good is it? I've tried to respond to this before, but I don't usually get very far; all of the answers I've offered have either been entirely theoretical or based in abstract aesthetics-- or both-- and, accordingly, have always been easily dismissed or denied. In this latest bout, however, I had slightly more information than before, and that small bit was enough to make me see that there is an objective response to the question.
First I had to challenge my own thoughts, and throw out the ones that simply did not pass the smell test. As the most important example, I've suggested before that people without absolute pitch are not truly "reading", and that they produce music only kinesthetically because they don't actually hear music in their minds. However, after a completely failed attempt to justify this speculation, I finally had to admit that it just doesn't make sense. For example, two musicians of my own close acquaintance are phenomenal pianists; the one can sight-read with clarity and expressiveness, and the other is a magician at improvisation (he will often play live for silent movies). How could I seriously claim that the former isn't sight-reading, or the latter isn't hearing the sounds in his mind? It's implausible to the point of impossibility. But if absolute pitch isn't responsible for "true reading", and music can be mentally conceptualized without absolute pitch-- or, more broadly, if absolute pitch does not have this kind of critical functional value-- then the only purpose I could argue for absolute pitch would be completely aesthetic, and totally subjective, and thus indefensible. I began to think that I would have to willfully suppress the "value and purpose" question until some kind of objective measurement could be devised, but it seemed too hollow to proceed with my work merely imagining that perhaps, maybe, someday, some magical hoped-for event would arrive to prove that absolute pitch had a reason to exist.
The answer hit me like the proverbial brick. I had been reviewing Diana Deutsch's latest publication; in it, she and her team reassessed the 2001 publication by Gregersen (et al) which claimed that [East] Asians were more likely than non-Asians to possess absolute pitch. Deutsch had the idea to distinguish between the Asians who grew up on the North American continent and the Asians whose native language was tonal; and sure enough, with this new segmentation there was no obvious difference between Asian or non-Asian, but there was a strong relationship with tonal language. Deutsch uses this data to re-emphasize her ongoing thesis, which is that learning a tonal language in childhood allows one to be sensitive to absolute pitch value. In her earlier publications she had suggested that linguistic tones carry over to musical absolute pitch because, for a listener who is already sensitive to absolute tonal value, musical pitches can be easily learned "as though they were the tones of a second tonal language." As I was reminded of this statement, it suddenly struck me-- what if music could be learned as a non-tonal language?
How can musicians be brilliant without absolute pitch? Well, how can English language be so rich and vivid and yet have no tonal qualities? To speakers of a non-tonal language, the pitch of a word is functionally irrelevant, but to a speaker of tonal language, a different pitch changes the meaning completely. That old chestnut, "Is a transposed song the same song?" would be answered yes by the non-absolute musician, and they would be perfectly correct, because their comprehension of music does not encompass the qualities which would make it different. But the transposition question is answered no by the absolute musician for the same reason that a Yoruban can find three different meanings in the word "owo". Like a repitched word in tonal language, a transposed melody may retain its structure, but communicate a different meaning, and, presumably, only those who perceive music as a tonal language will be objectively sensitive to this distinction.
This observation comes as a great relief to me, because I will no longer have to even attempt to answer why absolute pitch is "important" or "valuable" in music. Speculate all you want, argue all you will-- the fact is that nobody really knows, and among all my suspicions, expectations, and conclusions about reasons to covet absolute pitch I can't objectively defend a single one of them. What I can do is to point out that languages which possess no tonal qualities can be perceived, comprehended, and masterfully used, and this may explain relative musicians' ability to do perfectly well without absolute pitch; then there are also tonal languages, and absolute pitch values in those languages define the meaning of the word structures which transmit them. This parallel is enough, I believe, to strongly suggest that absolute musicians have an entirely different understanding of music than those without; and if that's the case, then I don't see why anyone would have to argue whether absolute pitch is a "skill" or an "ability" of any value.
How do absolute listeners detect the key signature of a melody? I'd vaguely imagined that they listen until they hear a note which sounds like the tonic, and then identify that tonic note by name. A couple days ago, though, I found myself describing an anecdote from Wilson (1911) which defies such an easy explanation.
We had been playing on his piano and had left his house and had cycled together some distance. passing a small house we heard a child playing a piano. My friend (who had absolute pitch keenly) asked me what key I thought the piece was in, adding that he was doubtful. I suggested A-flat and that it sounded like G and that the piano must be a semitone flat. He seemed to think so, too; but he argued that, if it sounded as G, why should it not be G? This we could not answer but could only say that we felt that it was A-flat. In order to satisfy ourselves, we wheeled round and got off at the house and looked in through the window which was close on the street. A glance was sufficient, the key was A-flat and the piano a semitone flat. Now, I think you will agree with me that the odds might have easily been against the child playing in four flats at all; but to make doubly sure my friend produced an adjustable pitch pipe and I fixed the pitch of the A-flat on this particular piano. On reaching home again, we found that this A-flat corresponded exactly with the G on his piano!
The author immediately follows his story with the challenge "If any of our readers can explain that, I should be interested." Perhaps now, almost a hundred years later, I can give it a try.
There isn't much to go on. In the entire history of musical research, there appears to be one and only one paper that explicitly recognizes the question of how absolute listeners detect musical key (Terhardt & Seewann, 1983). It's easy to find dozens of papers which discuss theoretical and structural tonality, or computer algorithms designed to calculate key signature-- but difficult to find anything that even acknowledges that absolute listeners can detect and identify the correct key signature of a given piece of music, much less one that tries to explain how they do it. Aside from the 1983 study (and its 1982 preface), the only experiment which even comes close is Corso (1957) who asked non-absolute musicians to identify key signatures absolutely. And... that's it. Incredibly, absolute key identification appears to be not just overlooked, but ignored.
The authors of the 1983 study didn't even ask its subjects to identify key signatures by name. Instead, for a given melody, they asked "is this higher, lower, or the same as key X?" Non-absolute subjects answered an average of 21% correct, which was slightly better than chance, but the average success rate of the absolute listeners is 93.7% (median 97%). The task isn't adequately difficult to generate enough errors to gain much insight into their strategies.
One anomaly did show some promise. For non-absolute listeners, the average identification rate was 20-40%, except for E-flat, which barely scraped 5%. Apparently, the E-flat excerpt sounded more like A-flat, and all 125 non-absolute listeners were consistently fooled.
the E-flat melody (1983): click image to hear
In a footnote, Terhardt describes how "[a]ll of the notes of the excerpt are
included in the A-flat major scale, while the note D-flat does not fit into the
E-flat major scale."
But none of the absolute listeners were fooled. They identified this melody just as easily as the others. This drastic difference between absolute and non-absolute respondents would be a promising result if it could be explained, and Terhardt speculated that
Non-AP-possessors, being unable to directly identify individual notes, evidently are dependent on a holistic feeling for key. In contrast, AP possessors in our tests did not actually have to find out whether the key of a test sample was right or wrong; they just had to aurally identify some individual notes and compare these with the score (nominal key) available to them.
Wait. What? A "score" was available to the subjects? What score? As soon as I read this paragraph I scrambled back to the procedure to learn, to my dismay: "a simplified, printed score of every sample in nominal key was provided to the subject." The absolute subjects weren't listening and deducing key signature-- they were reading off a printed sheet!
In other words, this experiment tells us nothing about how an absolute listener perceptually detects the key signature of a melody. To repeat from the above quote, they "did not actually have to find out whether the key... was right or wrong." Ultimately, then, this experiment tells us little more the patently obvious fact that an absolute listener can match aural tones to printed notes. And if this publication is indeed the only publication in history to even claim to address the method by which absolute listeners detect key signature-- which, unbelievably, it seems to be-- then we are firmly and unambiguously rooted on the proverbial Square One.
So I'm right back to my initial vague speculation, which is essentially identical to Terhardt's 1983 expectations. His sounds like a nice definitive answer, which is why I hadn't bothered to think much further about it:
What AP possessors primarily and immediately identify is musical notes, not keys. When asked to identify the key of musical samples, they perform quite well but need some time to infer the tonic from individual notes. ...The subject first identifies one or several notes of a musical sample and subsequently infers therefrom the tonic according to the rules of conventional musical practice.
But the problem arises-- what does it mean to "infer" the tonic? Maybe, as I had thought (and Terhardt implies), you hear a couple notes, decide which one's the tonic, you're done? Not quite. I asked my current roommate, who happens to be a classical pianist with absolute pitch, and he said
I usually listen for progressions. When I hear a tell-tale progression that's a dead giveaway. Sometimes instead I'll hear the leading tone and that will tell me.
Wanting to support Terhardt's (and my own) explanation, I asked my roommate if he doesn't "identify one or several notes" to make his judgment, but he said no. I rephrased the question a couple different ways-- don't you try to extract individual notes? do you wait to hear the one tone that's clearly the tonic?-- but each time he assured me the answer was no, no, no. He was certainly not "identifying one or several notes" to infer the tonic. Rather, he detected relative structures indicative of a key signature and identified their... what? Components? Scalar positions? "Key feeling"? I tried to understand as he explained, but it began to sound entirely circular; a progression identifies the key signature, you see, because the progression belongs in the key signature.
As I considered what he had told me, I remembered a curious experience I'd had while rehearsing Frog and Toad a couple months ago. To provide another actor with a starting pitch, the pianist struck a tone; I was pleased to immediately recognize the tone as A-flat, but then the full piece began and the sound of the A-flat persisted. I listened with astonishment to a sensation I had never before experienced. A-flat permeated the piece, sounding continuously, even though I could tell that the actual A-flat key was not being pressed. I don't mean that the song "felt like" A-flat in some fuzzy emotional way. I mean that every sound I heard was undeniably flavored with a palpable, audible, recognizable A-flat. I approached and was informed that yes, the song was written in A-flat major. At the time I had wondered if this is what it felt like for an absolute listener to recognize a key signature.
Now that I think about this event more critically, it seems to be the reverse of "one note" Interval Loader. In one-note games, Interval Loader plays a I-IV-V-I progression to set your mind to the appropriate key signature. This allows your mind to create the imagined sound of a tonic to add to the perceived sound of a single tone; by evaluating the resultant combination, you can identify the "top" tone which is the scale degree. But what if it worked the other way around, to identify the "bottom" tone instead? Consider: if scale-degree quality is a combination of perceived tone and imagined tonic, then hearing a tone and assigning it a scale degree automatically creates an imagined tonic. If you listened to a piece of music and, consciously or unconsciously, assigned scale degrees to the tones, then every single sound you heard would regenerate and reinforce the tonic pitch in your imagination and you would, therefore, be able to not only perceive the tonic but attend to it as a constant presence-- an unceasing flavor of sound, whether physically present or not, even as I heard the A-flat throughout that piano piece. Perhaps this could explain the circular logic of my roommate's explanation (leading tone notwithstanding). If you became aware that this imagined sound existed, and learned to listen for it (and to it), then perhaps it would indeed be simple and easy to identify the key signature of any piece of tonal music.
So if these scenaria were true, would they help explain the story from 1911? If the entire piano were lowered by exactly one half-step, then the boys could undoubtedly have heard a G as the key signature (as they would any key signature) because of the reverse-scalar effect; so the real question is, as the author says, "if it sounded as G, why should it not be G?" The explanation may lie in supposing how the piano was mistuned. According to Why Does a Piano Go Out of Tune:
During periods of low relative humidity the soundboard shrinks, reducing the crown and decreasing pressure against the strings. The pitch drops, again with the greatest effect noticeable in the center of the keyboard.
The boys only checked one single A-flat with their pitch pipe. Whether low humidity or some other reason, perhaps this single A-flat was in the center of the keyboard, in an area of "greatest effect"; maybe the other octaves were less detuned and still sounded closer to A-flat. If that were so, then every time the other octaves appeared in the piece they would "flavor" the G-major music with an imagined A-flat sound. Consequently, although the primary and evident tonality of the piece-- drawn from the middle octave-- would be a distinct and unambiguous G, that same G could sound like a leading tone.
So there may be the solution to a century-old mystery. What I'm left to wonder about is how someone without absolute pitch would have responded to this same piano. I believe it's been well-documented that any person's mind will quickly and readily adjust to be "in tune" with a musical key, regardless of that person's musical abilities; would they have noticed the strange mixture? Why does it even happen that non-musicians can adjust to a musical key signature? And if transposition of this type is indeed so easy, quick, unconscious, and natural that anyone can do it without any musical competence, why do people believe so strongly that absolute musicians can't sing or play an instrument in transposition? Some thoughts about these questions... next time.
I wanted to test the 1911 solution by simulating the mistuned piano. I took an A-flat melody and adjusted it microtonally to make the middle-octave tonic precisely in tune but, radiating outward, the tones gradually stretching to finally be 55 cents sharp. The melody was evaluated by an absolute musician who judged it to have a "A-flat, but not A-flat" sound to it, and his response would seem to support the possibility that a piano could be mistuned to produce "G, but not G"... except for one thing. The unevenly mistuned melody sounds so unbearably hideous that it seems unimaginable that the author of the 1911 story would have failed to mention its unpleasantness. I wondered if maybe adjusting everything upward by 25 cents would help even out the sound, and even though the upward-adjusted melody isn't quite as bad as the first it's still gratingly uncomfortable to listen to. Maybe the 1911 author, to make his own abilities seem more impressive, deliberately omitted the fact that the piano sounded so blatantly out of tune, or maybe there is a mathematical maladjustment and specific melody which makes a "leading tone tonic" possible without sounding so awful. It's not impossible-- but it is improbable enough to consider other answers.
Logically there would seem to be only one other answer: the melody must have "felt" wrong to the boys as they cycled past. Somehow, to them, this G-major melody felt like it should be A-flat... but why should the music seem to be in the wrong key? I am fully aware that absolute listeners will often complain that a transposed melody sounds "wrong", but in each example I know of the listener has had previous exposure to the melody and is comparing the new version to the remembered sound. The boys in the 1911 story don't indicate any familiarity with the tune being played, and if the author had recognized the melody then he surely would have found no mystery in the occasion. Something else must have done it, something besides the mis-tuning, and yet I think the piano may be responsible.
Admittedly, the melody could be the cause. You've probably heard of the "key feeling" of certain tonalities. A musical key may feel "bold and bright", or "sharp and taunting", or "smooth and moonlit", or whatever other subjective sensation a listener may assign. It is possible that whatever musical message was being transmitted, the boys agreed that the message would have been better expressed with an A-flat "feeling" rather than whatever they were getting from the G. This could be the reason, but if this is the reason, I don't yet know how I could try to explain it; after all, the key feeling is a subjective one to begin with, and if the melody were unfamiliar then why would the two boys decide and agree that it sounded "wrong"-- and by exactly one semitone? How can you tell that something is in the "wrong" key when you don't know what the "right" key is? I don't think these are necessarily rhetorical questions, but I think they can best be answered by again considering the piano, not the melody.
A normal human mind, regardless of its musical training, will naturally tune itself to a key signature. Even without brain scanning evidence, it's been known that non-musicians can detect as easily as musicians which chords don't belong in a given piece of tonal music, and non-musicians can evaluate musical "tension" and "resolution" with great competence. I think the reason for this universal skill can be readily observed in everyday life: every one of us speaks at a preferred tonic, and the emotional information communicated by our personal "key signature" is essential for the listener's understanding. It doesn't have to be subjective emotion, either: questions rise in pitch, introducing musical tension which must be resolved (presumably by an answer); statements end at a tonic, distinctly indicating the resolution of an idea. As an actor, I often have to speak monologues without losing the audience's attention; I have found that the easiest way to indicate "I'm not done yet" is to finish my sentence at some pitch other than the tonic. What's more, the further I land from the tonic-- the more musical tension I introduce-- the more intently the audience listens for a resolution. You can try this yourself now just by saying any sentence at all and finishing that sentence on some tone other than your preferred tonic; you'll hear that the more musical tension you create, the more intense your listener's expectation would become... until you hit the octave, of course, which becomes a resolution of a different kind (you can feel an obvious octave-dependent resolution effect if you use a sentence like "That's what I meant to say!") You could even read this sentence out loud, right now, to notice how a comma or a semicolon instinctively keeps you above your personal musical tonic; but at the period you come back home.
You can hear these principles at work in the video embedded below, if you ignore the bombastic political message and listen instead to the speaker's musical values. He begins with a list of statements about the opposing political party (0:08 to 0:40); the statements all end above his natural tonic, introducing enough tension for each to indicate he will continue and, furthermore, to conceptually join all the statements together as a single itemized list. Compare this with the statements about his own political party (0:58 to 1:15) which all come back to the tonic; not only does he thus imbue his statements with musical stability and resolution, but he is forcing his audience to hear the statements about his own party as though they were separate and independent actions (rather than a list). And if that weren't enough, notice how at 1:18 he modulates to a different key and then immediately begins to use that tonic; if you follow his modulation, "..arrangements for the Speaker." sounds like the completion of a thought at the new tonic, and if you don't, it doesn't.
This clip is interesting both for the musical tension it demonstrates and for the fact that you yourself can instinctively detect these musical tensions. It doesn't seem too far a stretch to surmise that the speaker himself had no conscious or deliberate plan to use them. But these aren't the reasons I chose to show this to you.
When I first encountered this clip, I thought to myself before he spoke two sentences: That's not his normal speaking voice. He's speaking higher than he normally would. But I wondered, how could I know that? I've never met the man before. I've never seen nor heard him speak; I never knew he existed until this clip appeared among the "Most Viewed" segments. I don't know what is "normal" for him, and yet I had almost immediately decided that his instrument was tuned too sharply. Having made my judgment, I listened carefully on the chance that his dialect was responsible for the higher sound-- New Yorkers do tend to speak with a raised pitch-- but no, the shift I was attending to seemed independent of the dialect placement.
After I'd puzzled about this for a while, wondering how on earth I could verify my observation, I sheepishly realized that I could just look for another clip of the same guy. So I did, and the very first hit provided confirmation. When you play the next video, you don't have to play it for very long at all to recognize that he is speaking in what seems to be his normal tonic, which is undeniably lower than the previous clip.
This suggests another possible solution to the 1911 problem. Maybe the melody didn't have the wrong "key feeling", and maybe the piano was perfectly in tune with itself. Perhaps instead, even as the overall tension of this politician's voice created a timbral quality which was recognizably too high for his body, the overall tension of the 1911 piano created a timbral quality which was recognizably too low for that particular instrument. You wouldn't need absolute pitch to hear that-- but you would probably need a sensitivity to the normal sound of an instrument to recognize that its normal sound had been transposed in one direction or the other.
Is it necessary to have expertise to detect the politician's transposition? Did you detect that he was speaking at an abnormal tonic? As an acting instructor, I need to be aware of when a performer is speaking with tension brought on by the stress of performance rather than the direct needs of their role; as a dialect coach, I need to be able to analyze how a person's vocal apparatus is contributing to their overall speech pattern. Being able to perform these separate analyses, and to separate their effects as I listen to a speech stream, may be what allowed me to unconsciously recognize (and then consciously determine) that this politician's voice was too high. On the other hand, maybe you did hear it and I don't need to suggest additional expertise-- perhaps anyone would have heard the "too low" quality of the 1911 piano despite not being able to name it G or A-flat.
But even if you didn't hear that specific too-sharp quality in the politician's voice, I'm confident that by merely paying attention you would certainly have heard his use of tonic and musical tension as I described it. With pathological exceptions, we're all experts at producing and interpreting scalar relationships regardless of key signature. We're all experts at musical transposition.
I think I can build on the previous article with some acting-style exercises. Acting exercises are easiest to do in person, when I can get feedback from you and detect by what you're doing whether or not my explanations have made sense; since I can't actually observe you I will try to be very specific.
Let your body relax to a comfortable repose; now speak an open vowel, such as "ah" or "oh". Don't attempt to sing; just sustain the vowel and notice the musical pitch of your voice.
Now tense as much of your body as you can-- arms, legs, torso, et cetera-- and sustain the same vowel. Don't try to sing, or to speak at a selected pitch level. Just release the vowel, and you'll notice that the musical pitch you're creating is higher than the pitch you made before.
This should be enough to demonstrate to you that, when you release a sound without deliberately attempting to create a specific pitch, your voice's natural pitch (and timbre) is directly representative of of your physical body state. Now,
In a relaxed, natural state, speak a short sentence (any sentence) and pay attention to the musical contour of the phrase.
Say the same sentence again, with the same meaning and the same intention, so that the same musical contour is re-created. Do not attempt to sing the pitches or intervals!
This should be very simple. The "meaning" is the literal meaning of the words, and the "intention" is your reason for speaking the sentence. An intention can be a "because"; for example, I can say "I want a sandwich" because I'm telling my friend I'm hungry. That's my intention. I could say "I want a sandwich" because I'm choosing a sandwich instead of a salad, but that would be changing the intention.
If you use the same intention ("because" statement) to speak the same literal meaning, you will hear yourself naturally and automatically generating the same musical contour (and rhythm). However, if you abandon the intention to focus on making your voice sound exactly like it did before, the sentence will become meaningless sing-song, so don't do that. If you use the intention and meaning to allow your sentence to happen naturally, you should be able to re-create the same contour as many times as you like without its becoming "stale" or meaningless. You may want to repeat your sentence a few times right now to feel that for yourself, or change the intention and feel how the musical contour changes with it. Now,
In the same relaxed state, speak the same sentence with the same intention and meaning (musical contour), and pay attention to your personal "key signature", or tonality.
Now tense your body muscles and speak the same sentence with the same intention and meaning (musical contour), and listen to the new tonality. Ask yourself, what emotional purpose is implied by the new pitch level? Does it sound angry? Frightened? Frustrated?
Now here's the meat of it: speak the same sentence with the same intention and the same meaning, but change the emotional purpose.
Make sure that you choose an emotion, let your body change to match that emotion, and allow the pitch level to naturally occur from your emotional body-state. Do not simply choose a random pitch level to speak at.
Here are some examples of changing the emotional purpose. If my sentence is "I want a sandwich", and the intention is I'm telling my friend I'm hungry, I could say it
- because it is a fact (placid)
- because he's been ignoring my request (angry)
- because I've been wanting one all day (eager)
- because I don't have any money (ashamed)
With each different emotional purpose, you will hear yourself naturally producing a different pitch level; and, if you retain the intention and the same literal meaning, you will produce the same musical contours. Say your sentence with various emotional purposes, and you will find yourself naturally transposing the same melody to different key signatures.
[If I were there listening to you, my primary concern would be that you not do this backwards. Your vocal musicality needs to be unconsciously generated by your intentions and body-states, not from consciously forcing or controlling the musical sound. The single most common problem of any would-be actor is that they attempt to say their words in a way which would be correct if an intention existed, rather than speaking with intention so the words may appear truthfully.]
As you might have guessed, this process is essentially the root of my understanding of musical transposition. The literal meaning of my sentence determines which sounds I will choose to speak, while my intention combines with that meaning to dictate contour and rhythm; if I wanted to get a message across, that's all I would require. As an actor, though, I need to do more than speak a meaningful message; I need to convey my emotional commitment to the performance. I could, if I chose, manipulate my intentions and the meanings of the words I speak, without activating any particular body-state, to suggest an emotion; or I could ignore or even contradict my body state by manipulating the musical sound of my voice to present the apparent emotional needs of a scene (I have seen hundreds of actors do each of these strategies, and audiences are rarely fooled). However, I find it more effective, more potent, and an overall more complete experience to induce the appropriate body-state and allow its tonality to inform the entire communication stream.
Is a transposed melody the same melody? You can now see that this is my answer: it is the same literal message, spoken for the same reasons, but with a different attitude. To show you what I mean, here's an audio segment from the video clip I posted last time, and the same audio segment ratcheted down to be closer to his normal tonic. In the second clip, nothing but the pitch is changed. As you listen to each one, just ask yourself, how does this person feel? What is their emotional body-state?
An instrument doesn't have an emotional body state. Not being made of flesh, an instrument obviously does not become physically calm or agitated or excited; so the physical difference from one key signature to another is merely that the notes have "shifted up" or "shifted down", and the most evident qualities of the timbre remain essentially the same. That is, if the essential origin of tonality is a physical body state, and instruments cannot change their body state, then different tonalities played on the same instrument will imply different physical-emotional attitudes, but can represent none of them directly as a human body would.
Should it be surprising, then, that musicians who produce music outside of their own body could become indifferent to absolute key signature?
"Do you spell words when you type?"
The questioner continued: "When I write longer words, I always spell them out as I type. Do you do that?" I didn't reflect long before telling her no, I don't. I can't prevent myself from chanting "Mississippi" thanks to grade school, but otherwise I don't spell any words when I type. I type in patterns. Sometimes I'll even type a wrong word because its first few letters trigger a more familiar pattern (such as "correctly" instead of "correlate"). Before being asked this question, I'd always assumed that my rapid typing speed was a direct function of touch-typing skill; but this person who types in letters was also a touch typist, and as she types at half my speed it seems now quite likely that the primary element could be the fact that, as an example, the word "familiar" is to me not eight keystrokes pressed in deliberate sequence, but a single gesture which rolls across the keyboard.
A person's typing strategy seems to remain consistent regardless of word length. For the person who asked me this question, there is a threshold above which words must be spelled, even when they are completely familiar; but for me, any length of word-- even non-English words, or English words which are so peculiar as to almost be non-words-- are processed and produced in syllabic patterns. Increasing unfamiliarity simply makes me more consciously aware that I am "speaking" each word in my head as I transcribe it. The only words I do type letter-by-letter, it seems, are those whose letters do not form obvious English syllables, such as "Kowalczyk" or other foreign surnames.
Are you a letter-typist or a syllable-typist? Do you type patterns or single keys? Leaving aside the (speculative) origins of these two strategies, their mere existence may describe, by parallel, the persistent debate about whether absolute musicians do or don't have trouble with transposition.
In musical transposition, tones are changed either by the instrument or by the musician. On a transposing instrument, a musician reads and plays as normal and the instrument automatically changes the sound; otherwise, notation is altered and fingering is physically shifted by the musician. Supposedly, absolute musicians find either of these methods difficult, while relative musicians find both to be effortless, and the exceptions are said to be those who prove the rule. But why should this be?
I myself can physically transpose on this computer keyboard, shifting my hands rightward by one key.
the rain in spain
yjr tsom om d[som (transposed)
The parallel to music does fail in the sense that the result of this "transposition" is meaningless, but the parallel does remain secure in the most important sense: shifting my fingers will produce sounds other than those originally intended, but I can nonetheless proceed effortlessly-- and I do this by attending to the sounds in my head which precede the keystrokes, not to the strange sounds that result. If I deliberately attempt to remember and type "tjr tsom om d[som", transposition is far more difficult than if I simply shift my fingers and type the familiar pattern of "the rain in spain."
In this perspective, musical transposition is nearly identical to stage-dialect work. Actors typically find dialect work extremely difficult because they do it by substituting sounds ("eh" not "ah", "ee" not "ih", et cetera). A substitution approach is laborious, because each individual phonemic alteration must be separately identified, tagged, changed, memorized, and implemented; a substitution approach is burdensome, because an actor must constantly struggle to remind themselves to say the "wrong" sounds; and a substitution approach is ultimately ineffective, because an actor becomes too occupied with generating target phonemes to be able to communicate naturally. These difficulties sound very similar to Miyazaki's description of an absolute musician trying to transpose with, as he calls it, "imaginally devised notation"; rather than shift the basic pattern of a melody, Miyazaki's absolute subjects attempted to memorize and recalculate each tone separately.

If a musician is a "letter typist", reading and producing music by the absolute notes rather than the patterns of those notes, then transposing will certainly be a tedious problem.
The most successful outcome does not occur by completely re-imagining a source to consciously produce its altered result, but by filtering a source through a production mechanism which causes an altered result to appear spontaneously. In dialect, this is achieved by changing mouth muscle usage, which may be analogous to physical transposition on a musical instrument; but in music it happens most easily, of course, when the "production mechanism" is a transposing instrument. The instrument performs the alteration, so the notes and the fingering are the same and the musician doesn't have to do anything differently. But when the notes and the fingering are the same, why would an absolute musician have any more difficulty than a relative musician? I think at least one answer can be found in dialect work.
The most difficult part of adopting a new dialect is in allowing words to come out "wrong". I don't mean words that are merely different, like "bingo" becoming "beenko" in Russian; those are rarely a problem because the component sounds are all present in some form. When the constraints of an accent make certain sounds impossible, however, words containing those sounds become stumbling blocks. When I performed in Dracula with a Dutch accent, I of course had to say the word "throat", and it kept coming out "twoat"-- an accurate Dutch pronunciation, yes, but I still felt stupid, because I knew that the "correct" word has "th" and "r" sounds. Despite my knowing that any accent would change the phonemes I spoke, I had to consciously accept that "twoat" was an appropriate way to communicate the word before I could allow myself to say it freely. It was still the same pattern-- I was trying to say "throat", it just came out wrong. I had to allow those unfamiliar sounds convey a familiar idea; but once I allowed it, the difficulty vanished. Once I allowed myself to accept that the communication stream was defined not by sounds but by patterns, not only did the difficulty disappear but I was able to monitor my output-- to hear how the new sounds fulfilled the same meaningful patterns-- without my becoming confused.
It seems probable to me that this describes, if not explains, how a musician may or may not have difficulty with transposition. Absolute or relative, the musician who transposes easily is the one who types in patterns, concerning himself only with communicating the message of the melody (and its harmonies); the musician who can't transpose is the one who either types by letters or, while successfully typing in patterns, doesn't apprehend how the new sounds may communicate the same musical concepts as before. I think it's possible that absolute musicians who have terrible trouble with transposition may be easily re-trained to accomplish it merely by encouraging them to produce patterns irrespective of the individual sounds. In dialect coaching, I say "let yourself be surprised by the sounds as they appear," and it's a potent statement; once a student allows this to happen, their entire understanding of dialect work changes. I'd imagine it likely that an absolute musician who "can't transpose" may simply have never been given training which acknowledges and accommodates their sensibilities.
Why would you transpose?
The most common answer I've seen is that transposition is merely a mechanical necessity. Musicians such as Ron Gorow have stated that key signature is an objective choice to begin with, determined by the technical limitations of whatever instruments a composer intended to use; and, when different instruments can't reliably produce the indicated notes, shifting those notes either "up" or "down" is a meaningless accommodation where nothing is fundamentally changed. You've heard this argument before, I know... as long as the relationships between the notes are the same, the melody remains the same, because the musical contour is intact. However, regardless of how strongly you agree or disagree with that statement, it can't be denied that transposition changes a song.
Transposing changes timbre. You don't need to change instruments to change timbre. If timbre is defined as the overtone series of a complex sound, then any transposition must generate a different timbre; obviously, different notes generate a different configuration of overtones, so by definition timbre must be changed. To address whether a transposed song remains the same, then, the essential question isn't whether or not the melodic identity is retained by notes or intervals, but rather: is timbre a fundamental element of musical expression?
Daniel Levitin, for one, seems to have answered yes. He has been quoted to say that "pop musicians compose with timbre; pitch and harmony are becoming less important." If tonal center is inherently a timbral quality, then selecting a tonal center is not artistically arbitrary; if a composer is sensitive to timbre, C-major versus D-major is as distinct a difference as choosing electric versus acoustic guitar. This need not contradict the notion that key signatures may chosen based on the mechanical needs of a particular instrument; perhaps instruments are being selected precisely because of the timbres they will provide in their preferred key signature.
However, a composer who is further aware of the timbral distinctions created by different key signatures has an additional expressive element at his disposal. This is illustrated by the New York politician in the previous videos; anyone has a normal body state which, through physical agitation or relaxation, may be transposed "up" or "down" without changing the meaning or intention of what's being said. While it is true that a person can indeed completely ignore body state and still get their point across, deliberate manipulation of body state can communicate a more sophisticated message. A composer who works with multiple instruments, writing an entire score, would undoubtedly want to be aware of how each instrument's timbre is affected by a particular key signature, and how the instrument thereby influences an orchestra's overall timbre; I recently spoke over lunch with a musician who assured me in his own words that, ideally, an orchestra should sound "like a single body."
If transposition is not a function of tone but of timbre, absolute musicians could potentially have greater mastery of it either as performers or composers. Revesz was the first to describe the separate theoretical qualities of tone chroma and tone height, but Patterson and Griffiths have been the first to argue that a separable tone height creates a truly two-dimensional model of pitch (a cylinder to replace the visually-misleading helix) and, consequently, an infinite octave. I suspect this might offer a better explanation of why absolute musicians are notorious for making octave errors; if you judged height and chroma separately, you might misidentify a C3.8, as its fundamental frequency is C3 but its height more closely resembles C4. The critical issue is that in this view, absolute musicians fail to make correct octave identifications not because they are ignorant of tone height but hyper-sensitive to it. Where a relative musician may identify only C3, C4, or C5, an absolute musician can hear and potentially identify an infinite variation of height between octaves 3 and 5. (This could also explain why absolute musicians tend to have unusually precise pitch discrimination ability.)
Theoretically, an absolute musician would therefore be able to transpose not only in the standard manner-- semitones up or down-- but also by manipulation of timbre. As a somewhat clumsy example of what that might sound like, I borrowed some of Phase 13's sound files to create this simple melody and then the same melody shifted up by approximately half an octave but with the same tone chroma. I have to acknowledge that I don't see how a within-chroma transposition could be physically accomplished without changing instruments... but it would seem to stand to reason that if transposition can, ultimately, be redefined as the same musical pattern given a different timbre, then the people who will be most able to do it will be those who are most fully able to perceive, comprehend, identify, and manipulate timbre.
The data is in. The participants were 7 absolute musicians, 8 non-musicians, and 9 relative musicians. In case you've forgotten what the experiment is (it's been a while): a participant listens to a microtonally adjusted, arpeggiated trichord ("X"), and then decides which of two subsequent choices ("A" and "B") matches the first. Repeat 674 times and that's the experiment. Here's the longer explanation if you want to read that too.
At the start, I expected overall peformance to be absolute > relative > non-musician, and that "non-musician" results would be at chance levels. Rob was surprised at my prediction for the non-musicians; since they don't have to identify anything by name, he asked, shouldn't the non-musicians be able to do as well as the musicians? I didn't think so; the non-musicians would be more likely to hear the trichord sounds as a single tonal mass rather than three separate musical sounds, and therefore-- especially since the change will always be in the "middle" of the shape-- find it extremely difficult to even hear the sound properly, much less make fine distinctions. This prediction seems to have been borne out, and these results are statistically significant.
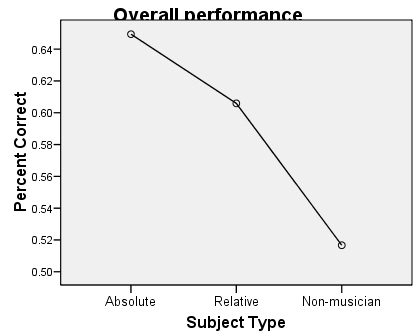
Statistical "significance", I've learned, is represented by the letter "p" (how it's calculated I'm not entirely sure-- for now I'm just glad that I know how to make SPSS do it); when "p" is less than or equal to .05, results are usually accepted as "significant". The "p" number essentially measures the likelihood that results are coincidence or chance, so the lower the better. In this case, the factor of "subject type" is p < .001, which means that there is a less than 0.1% chance that overall performance was not due to musicianship.
This experiment was originally created to test for categorical perception-- so was categorical perception evident? Well, no. Remember that if categorical perception is present, the graph will look like one of these guys:
And here are the actual results. There doesn't appear to be any obvious categorical perception going on here.
The non-musicians and relative musicians hardly seem to even hint at categorical perception-- and although the absolute musicians appear to have a smoother pattern, the peaks and troughs are in the wrong places. This result doesn't mean that musicians don't have categorical perception for chord sounds-- rather, if categorical perception exists, either this data doesn't show it or this way of looking at the data doesn't show it. Oh well.
So what did happen? However I look at the data, I keep coming up with the same answers: given the X-A-B presentation, it mattered whether the correct answer was A or B, and it mattered if the correct answer was higher or lower than the incorrect answer. Specifically...
When the correct response was B, participants did overwhelmingly better...
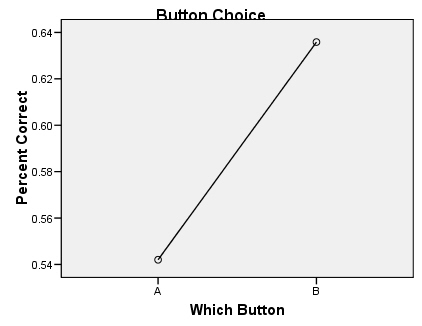
...but only if they were a musician. For non-musicians it made no difference; furthermore, a correct B-response had more of an effect on absolute musicians than relative ones.
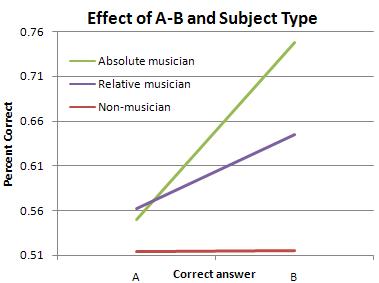
What's peculiar is that the condition we expected to have an effect-- shifting the entire chord upward by 25 cents-- did indeed have a statistically signfiicant effect, but only on the non-musicians. We thought the absolute musicians might be confused by chords whose pitches did not match a standard chord's intervals, but to them it made very little difference.
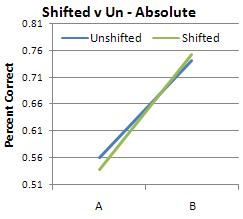
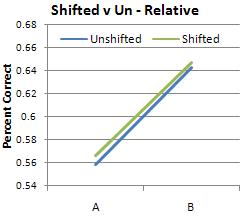
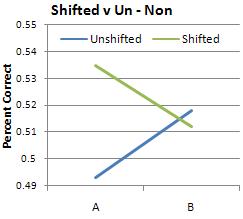
Next we take a look at "distance", where "distance" is measured as more or less in tune. The overall stimulus set can be represented by this diagram, where each vertical line is a different possible middle tone:
Taking only the middle tone into account (because the root and top are always in tune) would look like this:
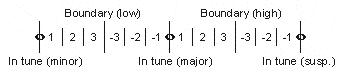
so each individual tone category can be represented like this...

In any trial, A and B are only ever one "step" apart-- so each A-B pair represents a "distance" of 1, 2, or 3 either down (flat) or up (sharp). If, for example, A were in tune and B slightly flat, that would be a "distance" of -1.
Statistically, absolute distance by itself is significant (p = .01). Here I mean "absolute" in the mathematical sense; in this next chart, -1 = 1, -2 = 2, and -3 = 3.
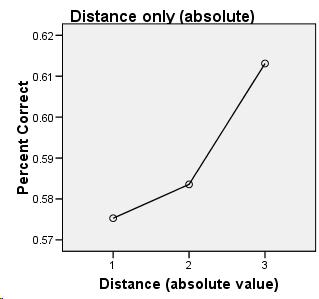
The chart of absolute distance clearly shows that being further out of tune makes it easier to judge. That same statement becomes even more significant (p = .005), though somewhat less visually obvious, when the distances are not mathematically absolute.
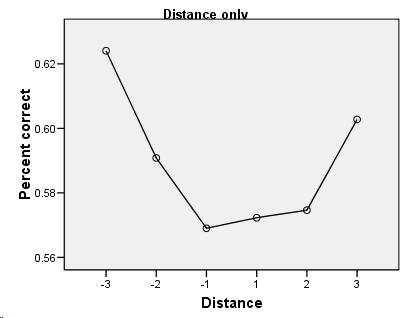
But that's not the end of the story. There is one factor which has a significant interaction with distance (p = .044): whether the "foil" was low or high. That is-- when a participant hears X followed by A and B, then one of those two is an incorrect response; the incorrect response is called the foil. The foil, obviously, will be either lower or higher than the correct response. Here's what it looks like when foil is separated into high and low:
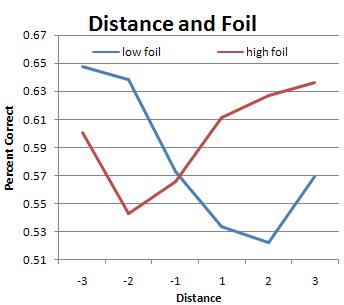
The fact that they're mirror images of each other, crossing at the "in-tune" point, seems to indicate that the low-high effect is consistent across the entire range... but what does it mean?
In short: participants tended to choose the response which was more in tune. Let's say, for example, that the choices were A or B as in the following diagram, where the middle line is an in-tune major chord.
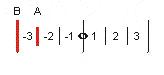
A participant faced with this choice would be more likely to choose A, regardless of whether or not it's the correct answer, because A is more in tune than B. Therefore, in this example, a participant will be more likely to "get it right" when the foil is low (B), simply because the correct answer happens to be the more in-tune response. Although there does appear to be some kind of boundary effect which makes judgment easier at a distance of 3 (causing the upswing of the lower lines in the chart), this boundary effect is still visibly less potent than the in-tune effect.
This interaction, between distance and foil, isn't influenced by the other factors I've tested. The influence of B-responses, although significant by itself, doesn't seem to affect this in-tune tendency (p = .25). The 25-cent mistuning shift isn't a factor (p = .50) probably because-- as all the tones are shifted equally-- a shifted chord sounds as in tune with itself as a non-shifted chord. It also didn't matter whether or not the participant was a musician (p = .23). This is what I found most interesting; even the non-musicians were biased toward the in-tune sounds, despite having had no training or experience to consciously recognize a properly-tuned chord.
So that's how the first experiment turned out. Overall, out-of-tune stimuli were easier to discriminate than in-tune stimuli. The participants were helped by B being the correct answer, depending on their musicianship; and they were biased toward selecting the better-tuned response, regardless of their musicianship.
Now... why did these effects happen-- and not others? I expect that attempting to answer these questions, based on the available science, will be the purpose of writing the research paper. I'm sure I will have to force myself to avoid side discussions, such as the hypothesis that absolute listeners are better at discrimination because they have separate timbre and chroma perception; trying to understand these effects will be enough.
Using vowels, the authors identified groups of "good" and "bad" categorizers; within these groups, they found that the "good" subjects exhibited an apparent magnet effect for prototypes, and the "bad" subjects for non-prototypes-- and furthermore, in an ERP study, the "good" subjects' brains responded differently to prototypes than to non-prototypes.
With harmonic chords, the authors found a perceptual anchor effect with a C-E-G prototype in just temperament. Mistunings of E or G appeared to interfere with each other, prompting the authors to conclude that the intervals rather than the pitches are salient for chord identity.
The authors found an apparent anchor effect in that a harmonic C-E-G "prototype" triad was easier to discriminate than a "non-prototype". However, the "non-prototype" chords were created by holding the C constant and sending the E and G substantially out of tune (as much as a semitone). Reading this paper makes me realize that one of the differences between my study and most others is that there are three available prototypes instead of only one.
There are a number of bits in this paper which provide support
I'll need. The basic thrust of the paper: the authors wondered if
the perceptual anchor effect was not due to a major chord being a natural
prototype, but due to the listeners' musical experience.
They theorized, and then showed, that musicians' and non-musicians' performance
in prototype and non-prototype conditions were the reverse of each other.
They show that amateur musicians' discrimination ability is essentially
identical to non-musicians, which justifies my transferring one self-identified
musician's data into the "non-musician" group.
They not only show that trained musicians treat prototypes as anchors and
amateurs treat them as magnets, but they offer a probable explanation with
support.
They cite a paper which shows that professional musicians can make
discriminations as fine as 2Hz, which could support my expectation that absolute
musicians' performance will be superior.
What it fails to explain, though, is why in our study the trained musicians do
not show a perceptual anchor effect. Even with the differences
between their experimental design and mine, their results would still predict
the trained musicians to have enhanced discrimination at the prototypes and
diminished discrimination at the boundaries, and that's the reverse of what
happened.
This paper offers an explanation for the observed asymmetry of going in-tune versus going out-of-tune: "[S]timuli are perceived with reference to sets of alternatives and... good stimuli have few alternatives. Specifically, when melodies are presented in scalar-nonscalar order, but not when presented in nonscalar-scalar order, the first melody evokes a small set of alternatives which the second melody often violates.
By using mistuned intervals, the authors show that absolute listeners use relative relationships to judge intervals; they do not listen to pitch classes and calculate the intervals.
The author points out something which I feel silly for not having realized: the "prototype" C-E-G chord is supported not only internally, but by the C-major tonal context. By varying the root tone, I believe I've presented chords which are "tonally ambiguous in all respects except the ordered relationships between its tones." Furthermore, in his experiment, he showed that more confusion and discrimination errors occurred when a dissonant tone was "anchored", that is, when the tone that followed it created tonal resolution. Perhaps this can help explain my experiment's "distance" factor, especially combined with the in-tune-foil factor.
Using rhythm, the authors demonstrate an asymmetry which is also observed in chords and melodies: "discrimination between coherent sequences and anomalous variants is better when the coherent version is presented first."
Boring showed that trained musicians had markedly finer discrimination than untrained listeners.
Although I think the assumptions behind these authors' experiment are flawed-- they believe that judgment of pitch, judgment of interval, and discrimination of pitch or interval are all essentially the same task-- they do show a lack of pitch anchors for absolute listeners and categorical discrimination for relative listeners. They also bring up the concept of "trace-context theory"-- namely, that people will base their judgments on an exact sensory memory (trace) or an "imprecise verbal label relative to the overall stimulus context" (context).
The authors show that musicians show categorical perception for intervals, and non-musicians don't; that is, the categories have been learned. The authors also suggest that increased uncertainty could be a factor in making less precise judgments.
These authors also show that with decreased uncertainty, precision in otherwise-categorical judgment increases until classical categorical discrimination essentially disappears. There's a common sense to it; with increased certainty there is far more information which can be ignored and far more cues as to which is the most salient change.
Adults discriminated small changes more clearly in non-prototypical conditions (i.e. non-native vowels); however, they did not do especially poorly when discriminating near a supposed prototype.
The authors verify a method of determining subjects' individual prototypes, and observe that people tend to choose "more extreme" phonemic exemplars than the versions they themselves produce.
Using phonemic stimuli in experimental designs that resembled XABX, the authors showed that their subjects relied exclusively on auditory data and did not show categorical perception, even when the task was made easier with longer delays and wider discriminations. The authors say that categorical perception in the auditory domain is typically tested by ABX design.
"[E]xperience in acquiring new categories can alter perceptual sensitivity." This article conducts four experiments to determine whether training increases discrimination sensitivity (it does) and whether previously undifferentiated dimensions become separated (they do). These experiments are used to suggest that the categories thus learned directly affect how we perceive sensory input.
Building on Goldstone's 1994 study, this paper suggests that within-category similarity may not be a direct result of category labeling. Even without explicit category labels, subjects learned that certain faces were more or less similar and, subsequently, were less able to tell the differences between within-category faces. The authors conclude that within-category judgments are made based on characteristics common to the category, while cross-category judgments are made based on differences-- and that the within-category objects are perceived differently as a result of these strategies.
This paper provides evidence that people will make judgments of objects' similarity based on either single characteristics or relationships between characteristics, depending on which are the most similar to each other. This suggests the possibility, in this experiment, that the subjects may be evaluating either the relationships between all three tones or the single tone in the middle.
Infants who were exposed to "good" phonemic exemplars were better able to correctly categorize non-prototypes. Exposure to off-model exemplars led to reduced performance. The authors believe this provides support for the idea that infants are indeed using the provided examples as categorical prototypes.
There seems to be a lot going on in this paper in terms of tuning, consonance, and perception thereof-- but the distilled upshot seems to be (and the authors italicize it themselves to indicate its importance): [interval] judgments represent some combination of beat-rate detection and semitone-fraction awareness. That is, if the detection of interval mistuning were only beat detection, then it would be much more difficult to detect mistunings to dissonant intervals, and if detection were only "width" awareness, it would be much more difficult to detect mistunings to consonant intervals; but it seems possible to make reasonable judgments of either by applying different proportions of each of these strategies.
The author speculated that if absolute listeners were listening categorically, then the function of their responses to a magnitude-judgment task would take on a step appearance instead of a curved one. And it did. One of the more interesting results is that when she explicitly instructed the absolute listeners to remember a tone only by its exact magnitude, they nonetheless persisted in remembering it as being slightly sharp or flat versus a standard musical tone, which could represent an "anchor" effect.
The authors found that, for quasi-musical tones presented in arpeggiated thirds, the Just Noticeable Difference was 10 cents, which is convenient because our experiment used divisions of approximately 15 cents each (2 pitch categories = 200 cents, divided by 13 units). The authors also noted that skilled listeners could use "beat cues" from the harmonic interaction of the tones, which is a principal reason that our tones were arpeggiated.
"Garner interference" is what happens when an irrelevant variation interferes with a subject's ability to make identifications along a relevant dimension. In this paper, the authors suggest that the interference occurs not because subjects are thrown off by the irrelevant value, but because they're comparing the current stimulus to the previous one. This could help explain why trained musicians in our experiment exhibited no anchor effects; the irrelevant dimension in this case was pitch height, and there were three prototypes rather than one, so the musicians could not become fixed on any particular prototype and compare the current trial with the previous one.
Three experiments purport to model Kuhl's perceptually-magnetized space around a vowel prototype; their charts make it appear as though stimuli lying nearer the prototype are absorbed into it, perceptually.
"Multidimensional scaling analyses revealed that the perceptual space was shrunk near the best exemplars of each category and stretched near the category boundary." They way they describe the spatial warping of a perceptual magnet is appropriate to my experiment: "the best exemplars of a category pull neighboring tokens closer in the perceptual space."
Apparently not. In different conditions, the phoneme-boundary effect came and went, but the perceptual magnet effect stayed constant... except when the subjects didn't have a strong sense of a "good" prototype, in which case the magnet effect was lessened. Considering the observed magnet effect among all subjects in my experiment, I wonder if a well-tuned interval is a natural prototype, or if people are just biased to choose the "better" sound, or if the going-out-of-tune asymmetry is most at work.
The author suggests that perception of pitch is highly influenced by tonal context-- not only the overall tonality but its relationship to the other tones with which it directly appears. Perhaps most interesting is the observation that unstable tones may "move to" more stable representations.
Part of the reason for using monkeys was to demonstrate that the prototypes are not biologically universal; language experience seems to be the most likely culprit. This paper talks about deviant stimuli being "assimilated" to a prototype.
Specifically, 6-month-old infants seem to show magnet effects for native vowels and non-prototype responses to non-native vowels.
Building (perhaps) most strongly on a 1996 paper, this publication suggests that perceptual magnet effects are developed from the plasticity of the brain; that, through training, a neural image is formed which essentially is a representation of the categories in question, so that perceptual space is not "warped" but is instead being responded to with adapted neurological bias.
This seems to be the paper which identified the likelihood of categorical discrimination and, furthermore, invented the ABX method of testing within and across boundaries.
Particularly of Kuhl's results. The authors ran similar experiments with different, non-magnetized results. They argue that the task is inherently misleading because the information is not presented in a meaningful linguistic context; can we therefore be sure that the idealized phoneme is in fact a "prototype" or merely a "good example"? They also found that Kuhl's stimuli were not necessarily all within the same phonemic category, and speculated that apparent magnet effects could have been due to categorical boundaries instead.
This experiment is the most superficially similar to the one I've undertaken; the authors varied the middle tone of a triad. The three main differences are that they only varied the middle tone between the minor and major position; their variations were arithmetic rather than geometric; and they played the triads simultaneously rather than arpeggiated. Nonetheless, their musically-trained subjects demonstrated heightened discrimination at the categorical boundary and a step identification function delineated at the boundary point.
The authors suggest that the perceptual magnet effect is not necessarily anything more than the already-observed tendency for within-category discrimination to be worse than cross-boundary discrimination. This supports part of the Lively/Psioni argument.
Adults and 1-year-old children demonstrated similar biases for detecting mistunings from the standard Western scale (as opposed to non-Western scales). 6-month-olds did not show the same bias, but this could have due to developmental issues rather than acculturation.
The authors played seven-note melodies to musicians (M+), musically experienced listeners (M), and non-musicians (M-). The melodies were based on either major, minor, or Javanese scales, and the fifth note of each was mistuned. M- subjects were unable to reliably detect the mistuning for any of the three scales; M and M+ could detect the mistuning for all three scales, and they were significantly better at detecting these mistunings in the context of a standard scale. This would seem to be a reverse result from my own results, which show that subjects are significantly better at detecting mistunings when the tone is more deviant from a standard scale; however, it could support the results if I supposed that the detection was due to strong expectations which pre-conformed the expected note to a particular standard, and the odd-scaled notes were heard without strong categorical prejudice.
This paper demonstrates that when people are asked to make identifications along a continuum, the perceptual variability along that continuum is decreased. This could be the process which gives rise to the "magnet effect"; if so, it would seem to suggest that the magnet effect would be more likely to be present during an identification task rather than a discrimination task.
Using chords, rhythms, and speech, the authors propose a kind of perceptual-anchor paradigm in which templates are formed and activated, such that off-model percepts generate "error signals" from the most nearly associated template. A subject's difficulty in making comparisons between off-model stimuli, they suggest, may be due to both of the stimuli generating equally large "error signals" from the same template. That is, the perception that they are different from the template outweighs the perception that they are different from each other.
The experiments strongly suggest that, when looking for similarities, people look at relationships between characteristics, while when looking for differences people use the raw characteristics. This, more than anything else, would be likely to explain the A-B effect in our experiment.
An overview of what it means to "categorize" a physical object. It seems that there is such a thing as a "basic" category (i.e. "chair") from which more specific categorizations can be formed (easy chair, deck chair, etc); in general a category exists when its members are not identical but are treated the same way. The nature of categorical identity, according to this author, depends on the integrality or separability of its members' attributes.
Absolute musicians demonstrate categorical identification of musical tones, while non-absolute musicians do not. Absolute musicians furthermore show preference, in reaction time, for the tones of the C-major scale.
Support for a physiological explanation for dissonance-- that the partials of dissonant tones excite, with "beats", areas of the basilar membrane which lie within a critical bandwidth of each other.
The authors failed to observe a magnet effect for German and English vowels (where the non-native vowel was assumed to be a non-prototype). They did, however, observe the asymmetry that performance was worse when going from non-native to native vowel; this could be either a non-musical example of the going-in-tune effect, or the commonly-encountered stimulus effect, or both (or more besides).
Further support for the idea that perceptual magnets appear in younglings due to language exposure. This article points out that vowel distinctions appear to develop sooner than consonant distinctions.
It seems that musicians will alter the "size" of an interval in different contexts; in isolation, large intervals will tend to "grow" and small intervals will tend to "shrink", but in melodic context the interval size may be altered by the immediate contour. In either case, this experiment shows that the interval perceived as "correct" may change according to context.
Using stimulus spaced apart by logarithmic cents (as opposed to mathematical Hz), Rakowski shows that absolute listeners' categorical perception for pitch fulfills both criteria for identification and discrimination. To achieve these results, though, he had to make the task very difficult-- he had to decrease the tones' duration from 700ms to 20ms, and increase the duration between trials from 1 second to 10 seconds. When the task was easier, absolute listeners got perfect scores.
The author reasons that for discriminating changes in melodic intervals, interval size is more salient, while for harmonic intervals "beats" are more salient.
Using linguistic structures and placement of objects as metaphorical representation, Rosch showed that people tend to assimilate to a prototype. That is, "996 is essentially 1000" but not vice-versa. Rosch also makes the point, though not in this paper, that there are "natural" reference points which are natural prototypes (such as, in my case, a well-tuned chord).
The authors use "family resemblance" to describe a higher-order feature of category membership which is not inherently observable in an object's physical criteria. To use one of their examples, the attribute of you drive it may be applied to car, truck, motorcycle or tricycle, but this is an attribute which may only be inferred and not observed directly. In addition to this point, they provide a strong definition of prototype: "The more prototypical a category member, the more attributes it has in common with other members of the category and the less attributes it has in common with contrasting categories. Thus, prototypes appear to be just those members of a category which most reflect the redundancy structure of the category as a whole."
The authors describe a hierarchy of categorization. Basic categories carry the most blunt information (chair); "superordinate" categories are more abstract (furniture) while "subordinate" categories become more specific (deck chair).
The authors didn't observe any prototype magnet or anchor effects, but did observe an asymmetry that subjects did better when the "standard" interval (first presented, as exemplar) was more in tune than the "comparison" interval (second presented, to be evaluated). These results might have to do with the fact that the standard and comparison intervals were transposed within each trial; the non-musician subjects had to be instructed that a transposed interval was "the same", and trained to recognize the similarity, before attempting the experiment.
People (adults and infants) were better able to recognize the difference between fifths and tritones than they were fifths and fourths, despite the fact that the difference between fifths and fourths is a semitone "wider" than for tritones.
These experiments demonstrate, to my great surprise, another example of the going-in-tune versus going-out-of-tune phenomenon. In this case, they showed that it's easier to detect a change from a simple ratio to a complex one (perfect fifth to tritone, 97% accuracy) than the other way around (51% accuracy). I found this difficult to believe-- shouldn't it be extremely obvious when you've changed from a tritone to a fifth?-- but I listened to it myself and yes, although it is indeed an obvious change, it's also obvious how it would be less detectable.
The authors re-analyzed data from prior experiments on musical discrimination, and determined that there was a processing advantage for musical intervals with simpler frequency ratios (they are "processed more readily"). Their analysis of simplicity places p4 > M3 > m3, which makes me wonder if I can see this a processing advantage in my experiment for augmented > major > minor chord. They also introduce the idea that simplicity of frequency ratio, rather than "distance", contributes to the perceived similarity between intervals.
With adults and 6-year-olds, the authors show (again) that it's easier to detect changes from simple to complex ratios than the other way around.
The authors used infants to minimize "enculturation" effects when testing simple versus complex frequency ratios. They discovered that, for both melodic and harmonic intervals, infants were better able to detect differences from simple ratios than from complex ones. They suggest that this probably represents an inherent bias toward tones with simple ratios; although they don't rule out the possibility that non-musical simple-frequency ratios could have been learned from occurrences in the natural environment, they point out that their being so learned would most likely represent an attentional bias, which would not contradict their view.
Subjects were played consonant intervals (fifths) followed by a probe interval which was either dissonant (tritone) or consonant (fourth). The fourth was consistently perceived as more similar despite its being twice as "distant" as the tritone. They argue that this means ratio simplicity is a better measure of similarity than is "distance".
"If the nature of the task compels subjects to use a labeling
strategy, categorical perception will be pretty much a foregone conclusion."
However, when category-labeling information is made inaccessible (by the XABX
paired design), the task "will produce no categorical perception at all."
The authors show that an ABX design produces a strong bias toward B = X;
additionally, they suggest that artificial stimuli will be less likely to
produce categorical perception than natural stimuli.
Apparently, when tones are played nearer and further apart in time, they seem to grow nearer or further apart in pitch as well. The author discovers that absolute listeners are not subject to this effect when tones are well-tuned, but they do succumb when tones are out-of-tune. This could certainly explain why so many of my subjects reported that the top or bottom tones changed (when they never did), but it may also suggest a reason why distance from the prototype resulted in better judgments: at the prototype, more musicians used a "context" labeling judgment, and at the boundaries, more musicians used a "trace" memory judgment.
Absolute subjects may switch between sensory and verbal coding strategies, depending on how far apart the stimuli are. At 1/10 semitone, they use a sensory strategy; at 3/4 semitone, they use a verbal strategy.
Musicians with strong absolute and relative pitch are able to make judgments of tone and interval, respectively, which are not influenced by context effects. Non-musicians were highly influenced by context.
Musicians were presented with slightly mistuned intervals and asked to identify them. Although the subjects were able to categorize the intervals accurately (95% or better), they failed to hear the mistunings. Apparently, it wasn't that they had difficulty detecting the differences at small mistunings; rather, they actually heard the stimuli as though they were in tune.
The authors observe that when tasks which require musical expertise are presented to non-musicians in the form of familiar tunes and melodies, the non-musicians perform and respond with expertise.
The authors noticed that the perceptual-magnet effect had never been tested with any vowels except [i]. They tried the same tests with [I] and discovered results that did not support a perceptual magnet for the vowel.
Although the authors were able to replicate Kuhl's results with the i vowel, they suspect that the results can be explained as easily by increased auditory resolution at certain spectral values as by theorized prototype magnet effects.
Discrimination is stronger-- that is, small changes to a melody are easier to detect-- when there are more harmonics present in each tone than when there are fewer; furthermore, harmonics which are more consonant to the fundamental help more than those which are less consonant.
Another demonstration that it's easier to detect a change from a simple to a complex ratio (e.g. fifth to tritone) than the other way around. Infants and adults both do it, which suggests that it is not an effect of acculturation.
The title holds true in their experiment, whatever the reason for it. I say "whatever the reason" because this might represent the attentional bias described by Schellenberg and Trehub (1996b).
In a task which required adults and infants to detect violations of melody which either conformed to or deviated from their tonal context (C-major), adults were poorer at detecting conformed violations (i.e. B substituting for G) than deviant violations (i.e. A-flat instead of G) while infants were equally good at either. Furthermore, adults were confident in saying that G to B was a "smaller" interval than G to A-flat, even though the "distance" is actually wider. One possible interpretation of these results is that infants do not have a sense of "key signature".
There's something here about pattern encoding that I can't quite put my finger on. When a melody is transposed by a fifth (a tonally-related key), infants notice melodic changes more readily while adults' performance becomes worse. Could it be that adults retain some kind of global "tuning" which somehow supercedes the melody? I can't quite tell.
The authors make the specific conclusion that a perfect fifth may be a "natural prototype", based on the superior detection of changes to the "top note" of each of these chords. Another way to look at the same results-- which doesn't necessarily contradict the authors' speculations-- is that the former task is going in-tune to out-of-tune, while the latter is out to in, and Schellenberg would have predicted better or worse for that reason.
"[S]timulus naturalness is certainly a factor contributing to categoricalness of perception. This conclusion means that it is important to aim for stimuli that are as natural as possible."
This paper seems to show that a listener's judgment of a phonemic sound as a "good prototype" can be dependent on how the sound is generated.
This paper helps explain why the tones in my experiment needed to be arpeggiated: "Listeners can resolve the frequency of any one of the temporal components of certain word-length acoustic patterns only slightly less accurately than if those components were presented in isolation. However, they can only achieve this accuracy for early or low-frequency components when the listening conditions allow them to attend selectively to these specific elements."
I'm not exactly sure what to make of their specific results, but the authors make an interesting distinction between different types of coding and memory strategies for categorical perception.
Like Trainor's, this paper shows that infants prefer to listen to consonant sounds and not to dissonant ones.